이번 포스트에서는 최근 자연어 처리 분야에서 각광받는 대용량 언어 모델들의 기본 구성 요소가 되는 신경망 모델인 Transformer에 대해서 다룬다. 먼저 Transformer이 처음 나오게 된 계기인 기계 번역 태스크에 대해서 정리하고 어떤 흐름을 통해서 Transformer이 등장하게 되었는지까지 다뤄볼 계획이다.
목차
- 기계 번역과 Sequence-to-Sequence 모델
- Sequence-to-Sequence 모델의 문제점
- Attention 메커니즘
- Transformer
- Self-Attention을 통한 이점
- 기계 번역 결과 분석
- 정리
- 참고 자료
- 수정 사항
기계 번역과 Sequence-to-Sequence 모델
이전 포스트에서 기계 번역에 대해서 간단히 다뤘었다. 기계 번역은 특정 언어로 주어진 문장을 목표 언어로 번역하는 태스크를 말한다. 예를 들면 한국어를 영어로 번역하는 기계 번역 태스크가 있을 수 있겠다. 기존 딥러닝 기반의 기계 번역은 보통 입력 문장을 인코더(Encoder)를 통해서 인코딩을 수행하고 이 인코딩된 표현을 바탕으로 디코더(Decoder)가 목표 언어로 다시 재생성하는 방식을 채택하였다. 이를 가장 잘 수행했던 모델은 바로 RNN 기반의 Sequence-to-Sequence(seq2seq) 모델이다.
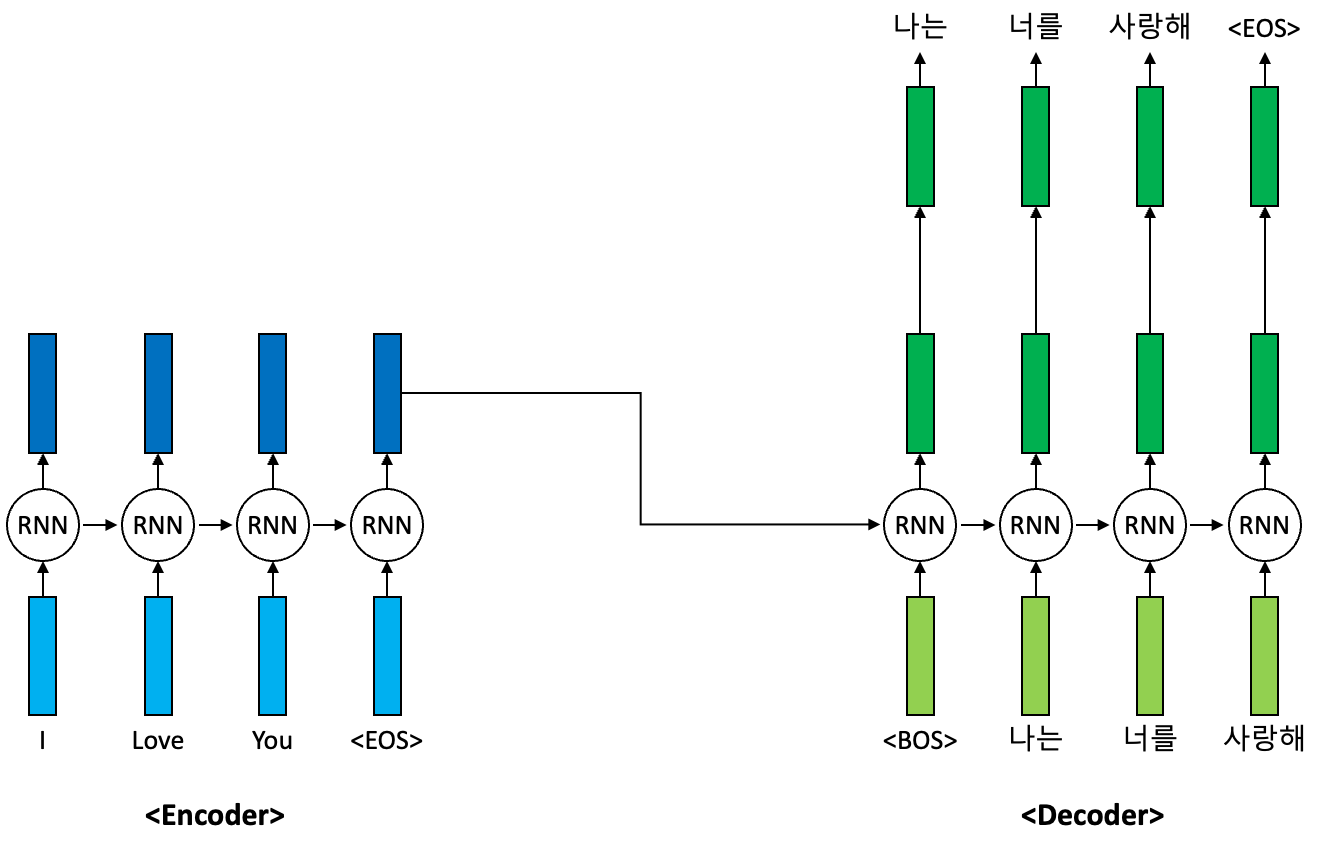
위의 그림은 영어 문장을 한국어 문장으로 번역하는 seq2seq 번역 모델의 예시를 나타낸 그림이다. 먼저 주어진 입력 문장은 RNN 기반의 인코더 모델을 통해 인코딩이 수행된다. 보통 인코딩은 마지막 <EOS> 토큰의 입력에 대한 인코더의 은닉 표현(Hidden Representation)을 인코딩의 결과 표현으로 활용한다. 이는 디코더 RNN 셀의 초기 은닉 상태(Hidden State) 벡터로 활용되어 디코딩 과정에서 문장 재구축에 활용되게 된다.
Sequence-to-Sequence 모델의 문제점
일반적으로 심층 신경망의 계층이 많아질수록 훈련 과정에서 뒤쪽 계층에 비해서 앞쪽 계층의 가중치 변화가 점점 적어지면서 앞쪽 계층의 가중치가 훈련이 잘 되지 않는 문제점이 발생하곤 한다. 이를 Vanishing Gradient 문제라고 하는데 이 원인은 심층 신경망의 계층 사이사이의 활성 함수(Activation Function)로 인하여 가중치의 Gradient의 절대값이 앞쪽 계층으로 갈 수록 감쇄하기 때문이다. 활성 함수로 많이 쓰이는 Sigmoid 함수의 Gradient 값은 항상 0과 1 사이의 값을 갖고 이 값이 자꾸 곱해지는 것이 반복될수록 Gradient 값 역시 감쇄가 일어날 것이다. 이러한 문제를 해결하기 위하여 Sigmoid 함수 대신 ReLU 같은 함수들을 활용하는 방향으로 연구가 되어왔다.
이는 기계 번역같은 태스크에서 쓰이는 RNN 기반의 모델에서도 많이 발생하는 문제이다. 입력 시퀀스는 시간 단계를 따라가며 반복적으로 RNN 셀에 입력이 들어가고 이는 최근 입력값에 대해서보다 이전 입력값에 대한 Gradient 절대값이 매우 작게 되는 현상들을 발생시킬 것이다. 특히 RNN 셀의 내부에서 활성 함수는 Sigmoid와 그 특징이 유사한 Tanh 함수를 사용하기 때문에 이 현상은 더욱 심할 것이다. 이 문제를 Long Term Dependency라고도 한다.
즉 입력 시퀀스의 길이가 길어질수록 긴 입력 시퀀스에 대해서 고정된 크기의 은닉 상태 벡터로 정보를 입력함에 있어서 정보의 손실이 발생하고 이는 너무 긴 길이의 의존성, 다시 말해 Long Term Dependency를 적절히 인코딩하기 어려워 현재 입력값에 비해서 이전 입력값에 대한 훈련 정보는 점차 사라진다는 결과로 나타난다. 결국 이로 인하여 모델이 시퀀스를 바라볼때 최근 입력값에만 집중하는 현상이 벌어진다. 이는 기계 번역 뿐 아니라 문맥을 활용해야하는 다양한 자연어 처리 태스크에서 그 문제를 발생시키곤 했다.
Attention 메커니즘
이러한 seq2seq 모델의 문제점을 해결하기 위해서 등장한 것이 바로 Attention 메커니즘이다. 기존 seq2seq 모델의 단점이었던 너무 멀리 떨어진 입력값에 대한 영향력이 너무 낮아진다는 문제점을 해결하기 위해서 멀리 떨어진 입력값에도 충분한 가중치를 부여하여 디코딩 과정에서 활용하겠다는 의도가 반영된 것이 바로 이 Attention 메커니즘이다. Attention 메커니즘은 본 블로그의 포스트들([Attention] Bahdanau Attention 개념 정리, [Attention] Luong Attention 개념 정리)을 참고하면 더 자세히 확인할 수 있다.
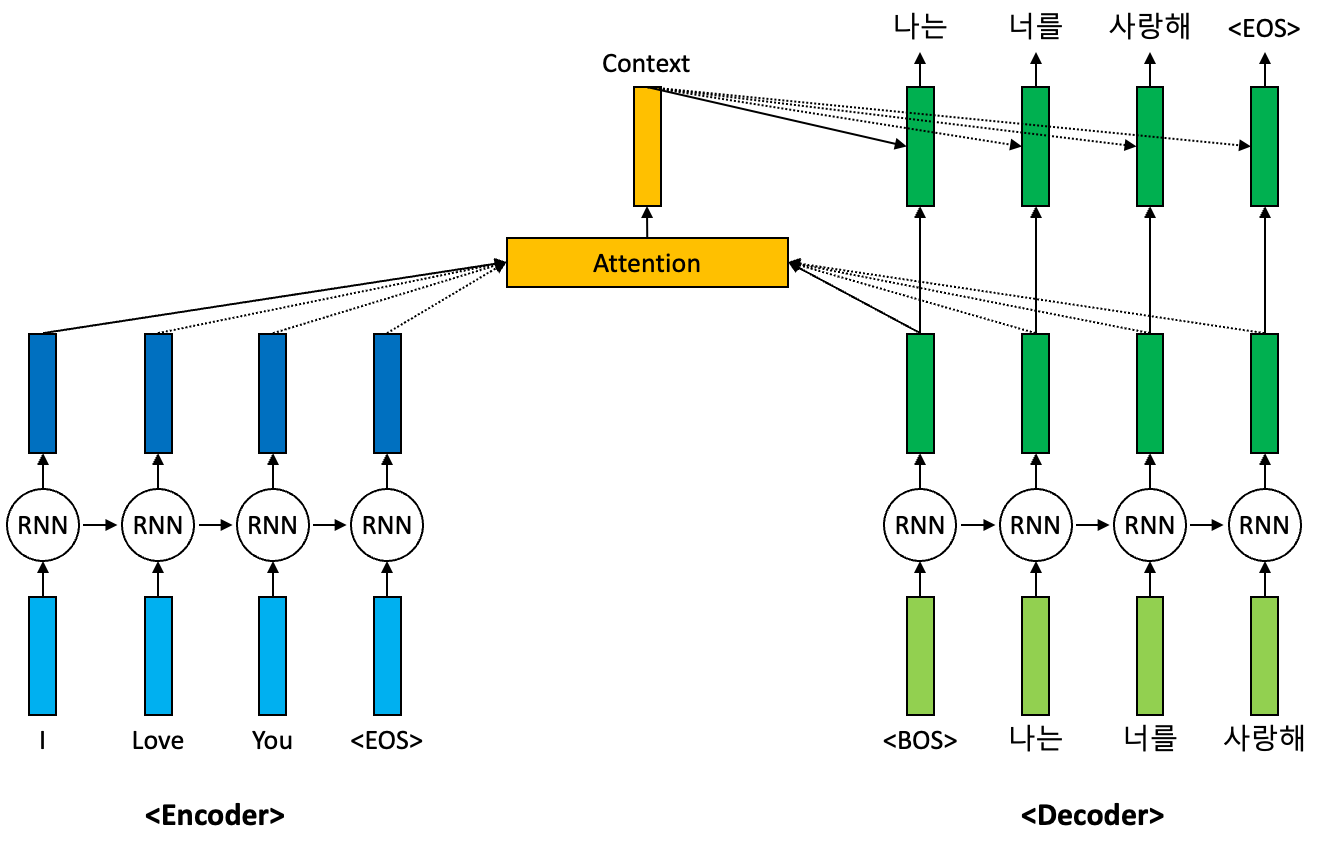
심층 신경망 기반의 seq2seq 모델은 기본적으로 입력 특징을 적절한 은닉 벡터로 인코딩을 수행하고 이를 디코더가 다시 출력 특징으로 변환하는 과정을 수행한다. 이 과정에서 디코더는 디코딩 과정에서 더 중요한 입력 특징들을 스스로 찾아내서 집중하려고 시도한다. 위 그림을 바탕으로 예시를 들어보자. 디코더는 입력 특징들인 “I”, “Love”, “You”, “<EOS>” 토큰 시퀀스를 바탕으로 디코딩을 수행한다. 여기서 디코딩을 시작한다는 의미의 “<BOS>” 토큰을 입력받은 디코더는 이 입력 토큰을 바탕으로 번역된 문장의 맨 처음 토큰을 생성하려고 시도한다. 예시에서는 “나는”이 될 것이다.
디코더는 이 “나는” 토큰을 생성하기 위해서 입력 특징들 “I”, “Love”, “You”, “<EOS>” 토큰 시퀀스의 정보를 활용한다. 이 과정에서 더 중요한 특징들을 스스로 찾아서 집중하는 현상이 일어나는데 Attention 메커니즘은 이를 좀 더 수월하게끔 구조적으로 설계하는 방법론이다. Long Term Dependecy를 반영하기에는 Vanishing Gradient 문제가 발생하기에 모델이 스스로 가중치를 선택하여 Vanishing Gradient 문제가 발생하는 긴 경로를 생략하고 직접적으로 멀리 떨어진 입력값에 집중할 수 있도록 도와주는 것이 Attention 메커니즘이다.
Attention 메커니즘은 기본적으로 Attention 점수를 계산하는 것으로부터 출발한다. 이는 일반적으로 현재 주어진 디코더의 입력값에 대한 은닉 벡터와 인코더의 입력값 전체에 대한 은닉 벡터들 사이의 내적을 통해서 계산한다. 위의 그림에서 인코더 입력 토큰들 “I”, “Love”, “You”, “<EOS>” 토큰들에 대한 인코더 은닉 벡터를 각각 \(\mathbf{h}_1, \mathbf{h}_2, \mathbf{h}_3, \mathbf{h}_4\)라고 하자. 또한 디코더 입력 토큰들인 “<BOS>”, “나는”, “너를”, “사랑해” 각각에 대한 디코더 은닉 벡터를 각각 \(\mathbf{s}_1, \mathbf{s}_2, \mathbf{s}_3, \mathbf{s}_4\)라고 하자. 여기서 디코더 입력 토큰 “<BOS>“에 대한 인코더 입력 토큰 “You”의 Attention 점수는 다음과 같다:
여기서 디코더 입력 토큰 “<BOS>“에 대한 모든 Attention 점수의 벡터화인 Alignment 벡터는 다음과 같이 정의한다:
여기서는 “나는” 토큰을 생성하기 위해서 입력된 디코더의 입력 토큰 “<BOS>“에 대한 Attention 점수를 뽑은 것이기에 아마도 인코더 입력 토큰 “I”의 Attention 점수가 가장 높을 것이라고 추측할 수 있다. 좌우지간 Alignment 벡터는 인코더의 입력 토큰 시퀀스의 길이가 \(L\)인 경우에 디코더의 \(t\)번째 입력 토큰에 대해서 다음과 같이 일반적으로 정의할 수 있다:
\[\mathbf{a}_t = \left[ a_t^{(1)}, \cdots a_t^{(L)} \right] = \text{Softmax} \left( \left( \mathbf{s}_t^\text{T} \mathbf{h}_j \right)_{j=1}^L \right) \in \mathbb{R}^L.\]이렇게 정의된 Alignment 벡터 \(\mathbf{a}_t\)는 디코더 입력의 \(t\)단계에서의 토큰에 대한 인코더 입력 토큰들 전체에 대해 Attention 점수를 나타내는 벡터라고 보면 된다. 모두들 알고 있듯이 \(\mathbf{a}_t\)는 정상화(Normalization)되어있기 때문에 모든 성분의 합이 1인 것을 확인할 수 있다. 이렇게 구해진 Attention 점수들은 인코더 은닉 벡터들인 \(\left\{ \mathbf{h}_j \right\}_{j=1}^L\)와 가중 합계로 계산되어서 문맥 벡터(Context 벡터)라고 불리우는 표현으로 변환된다:
이 문맥 벡터는 디코더가 현재 단계 \(t\)에서의 디코더 출력을 생성하는 떄에 사용되게 된다. 즉 이를 통해서 모델은 문맥 벡터로 활용될 인코더 입력 토큰들에 대한 정보를 어느 정도 수준으로 선택할지 가중치를 스스로 부여할 수 있도록 학습이 이루어지게 되며 결과적으로 매우 긴 입력 시퀀스에 대해서도 이전보다는 높은 수준으로 Long Term Dependency를 잘 반영하여 정보를 인코딩할 수 있다.
Transformer
Transformer는 Attention Is All You Need라는 논문에서 처음으로 제안한 Attention 기반의 심층 신경망 모델이다. 기존의 RNN 또는 CNN 기반의 모델들에서 탈피하여 오직 Attention 메커니즘만을 기반으로 하는 새로운 모델이다. Transformer는 등장하자마자 모든 언어 모델들의 기반이 되는 역할을 하였고 단순 자연어 처리에서 뿐 아니라 시계열 데이터를 다루는 음성 영역, 더 나아가 영상 영역까지도 활용되는 매우 중요한 모델이 되었다.
인코더-디코더 스택
대부분의 심층 신경망 기반의 시퀀스 변환기는 seq2seq 모델의 형태를 가지고 있으며 이는 구조적으로 인코더-디코더 구조를 따른다. 이와 마찬가지로 Transformer도 인코더-디코더 구조를 따른다. Transformer는 기존 인코더-디코더 구조와는 다르게 Self-Attention 기반의 스택 구조의 인코더-디코더 구조를 갖고 있다.
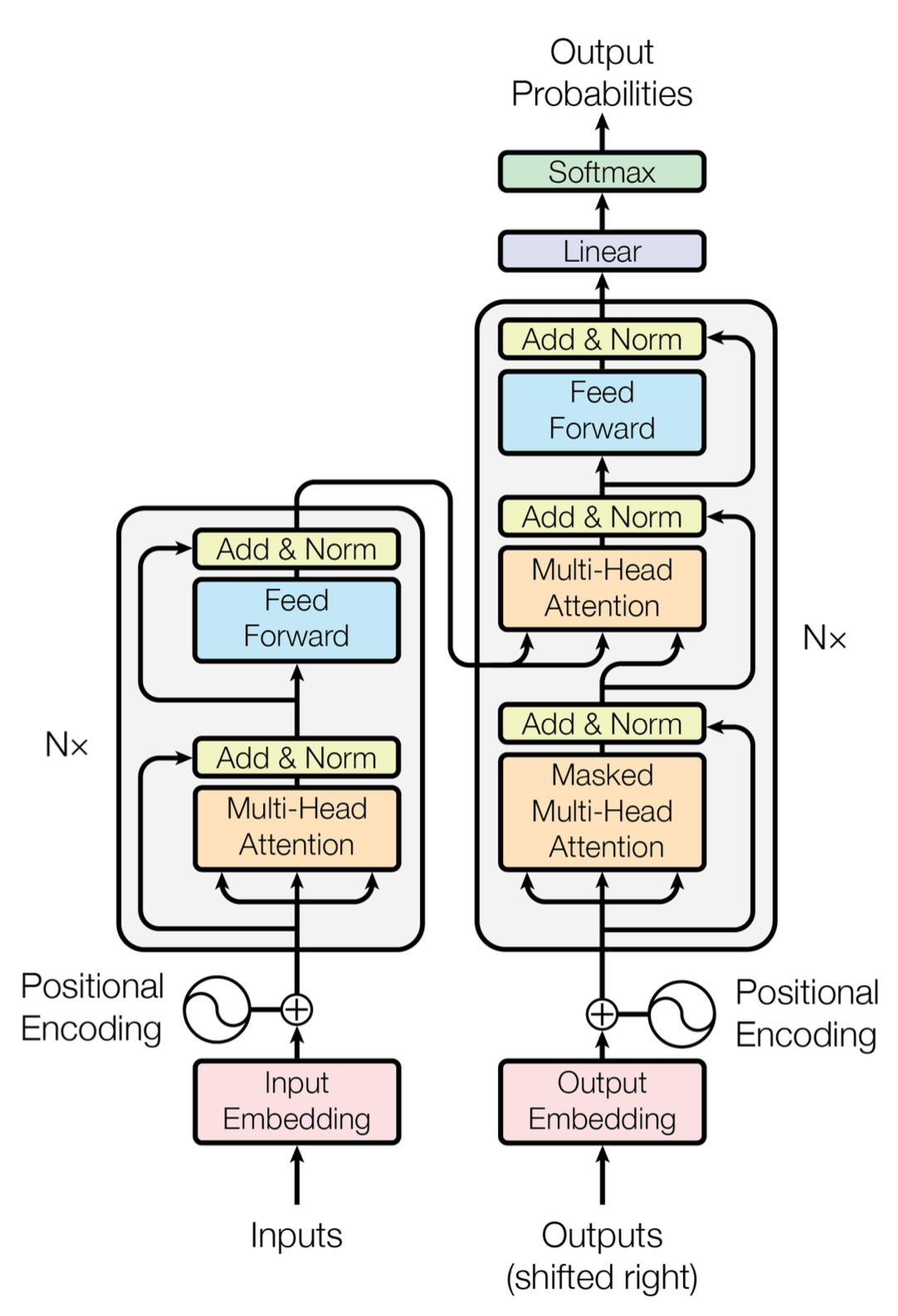
위의 그림은 논문에서 소개하는 Transformer 모델의 구조를 나타내는 그림이다. 인코더는 기본적으로 여러개의 동일한 계층을 쌓은 형태의 스택으로 구성되어 있다. 각각의 계층은 두 개의 보조 계층(Sub-Layer)로 구성되어 있다. 첫 번째 보조 계층은 Multi-Head Self-Attention 메커니즘이고 두 번째 보조 계층은 간단한 위치별 완전 연결 순전파 망(Position-Wise Fully Connected Feed-Forward Network)이다. 완전 연결 순전파 망이 위치별로 구성되어있다는 의미는 위치별, 즉 토큰별 은닉 벡터들을 동일한 가중치를 통해 투영하는 계층이 존재한다는 의미이다.
디코더는 인코더와는 조금 다르게 Multi-Head Attention 보조 계층이 두 개가 있다. 첫 번째 Multi-Head Attention 보조 계층은 인코더와 마찬가지로 Self-Attention 구조이며 차이점은 마스킹(Masking)이 되어있다는 점이다. 디코더 마스킹의 역할은 디코더 훈련 과정에서 입력 시퀀스에서 현재 시점과 그 이전 시점만을 디코더가 활용할 수 있도록 하기 위함이다. 추론 과정에서는 미래 시점을 확인할 수 없기 때문에 마스킹이 굳이 필요하지는 않다. 훈련 과정과 추론 과정 사이의 차이는 아래 그림을 통해서 확인할 수 있다. 훈련 과정에서는 필연적으로 마스킹이 필요한 것 역시 확인할 수 있을 것이다.
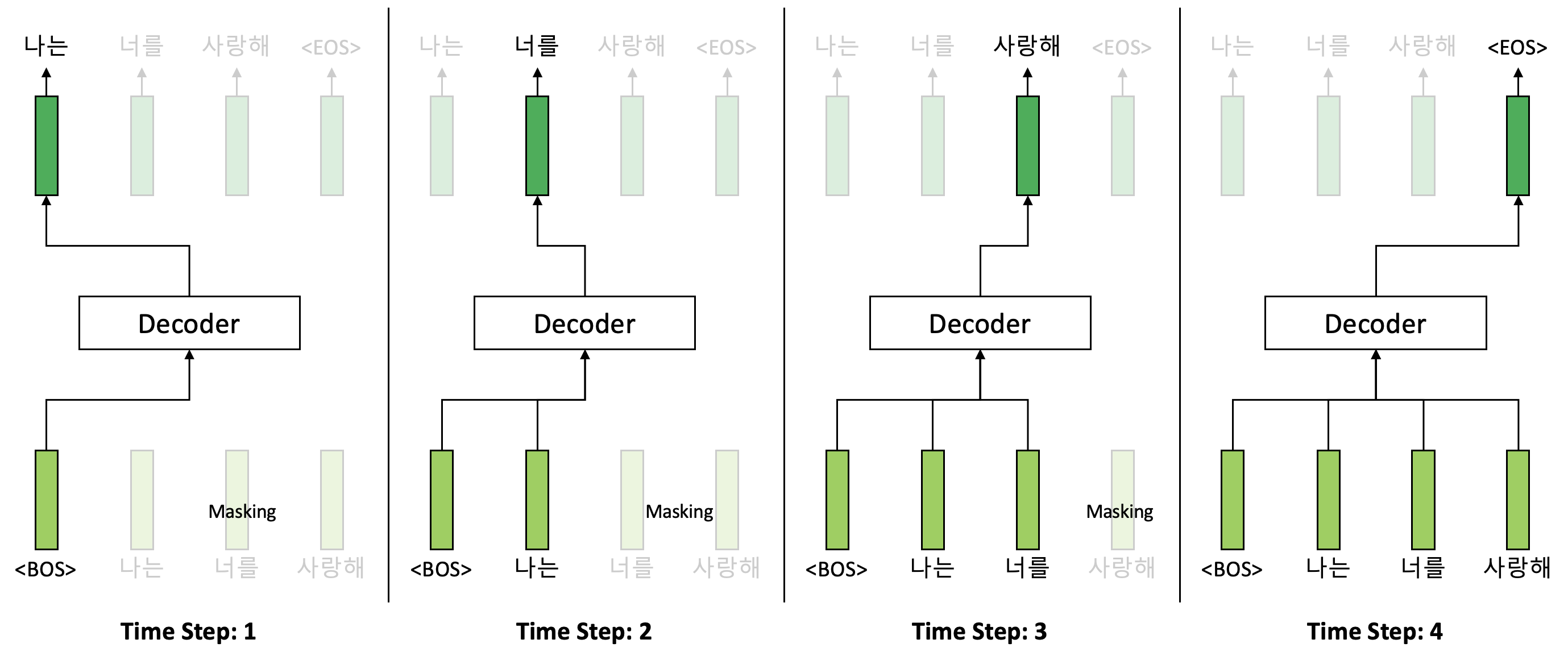<디코더 훈련 과정에서의 마스킹>
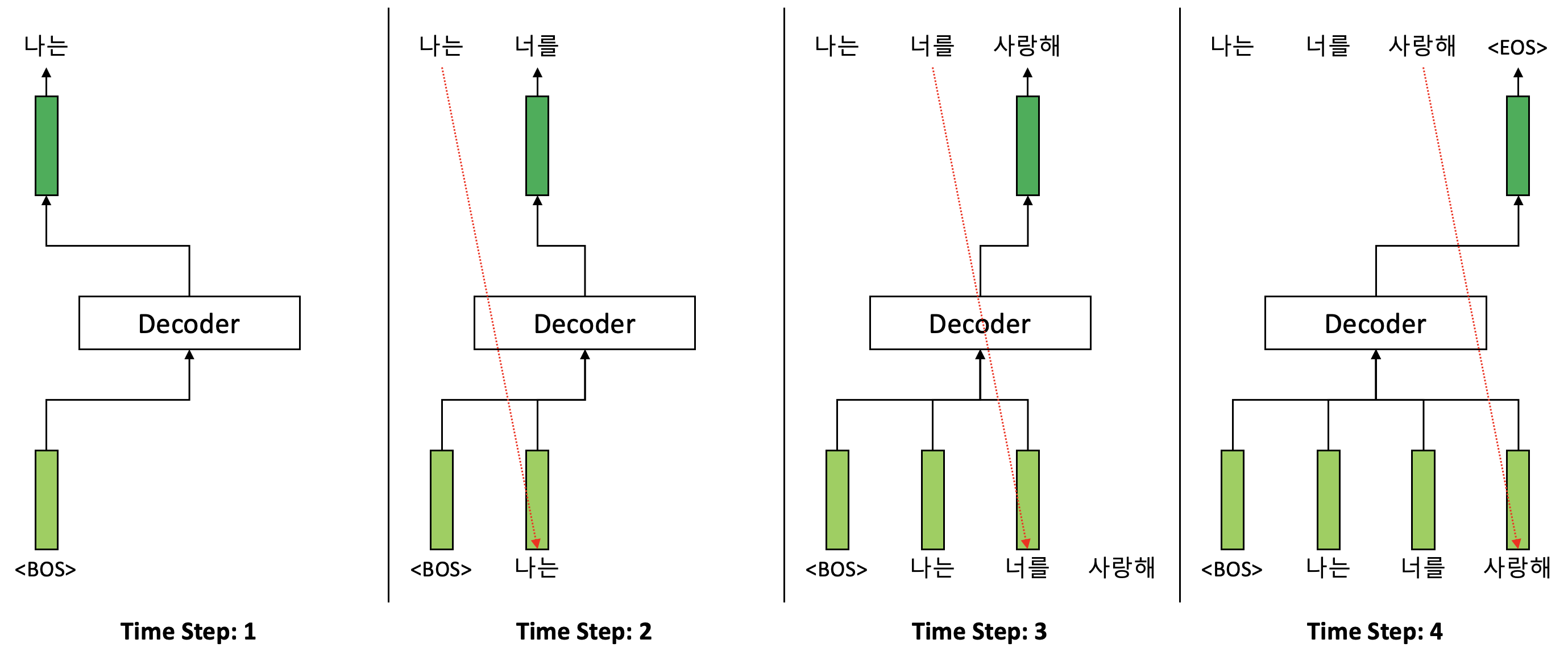<디코더 추론 과정>
디코더의 첫 번째 Multi-Head Attention 보조 계층을 통해서 디코더의 입력 토큰 시퀀스에 대한 은닉 벡터 시퀀스가 생성되고 이는 두 번째 Multi-Head Attention 보조 계층의 입력으로 활용된다. 이 과정은 Self-Attention이 아니며 인코더의 출력인 은닉 벡터 시퀀스를 함께 입력으로 받아서 Attention을 수행한다. 여기서의 Attention 함수에 대해서는 아래에서 좀 더 자세히 다뤄보도록 한다.
보조 계층 각각의 출력에는 Residual Connection이라는 연결과 Layer Normalizataion이라는 정상화 방법론이 적용되었다. Residual Connection은 입력과 출력을 한 번 더하는 방식으로 출력 연산을 추가하여 Vanishing Gradient를 줄이는 방법론이다. Layer Normalization은 Batch Normalization과 유사한 방법론이며 나중에 한 번 다뤄보도록 하겠다. Batch Normalization에 대해서는 다음의 포스트를 참고하면 된다.
Attention
Transformer의 Attention 함수는 기본적으로 벡터 형태인 Query, Key, Value를 바탕으로 주어진 Query와 Key-Value 쌍으로부터 출력으로 매핑하는 함수라고 생각할 수 있다. 주어진 Query에 대해서 모든 Key 값들과 Attention 점수를 계산하고 이를 가중치로 하여 각각의 대응하는 Key 값에 할당한다. 이러한 방식의 Attention 메커니즘을 저자들은 Scale Dot-Product Attention이라고 부른다.
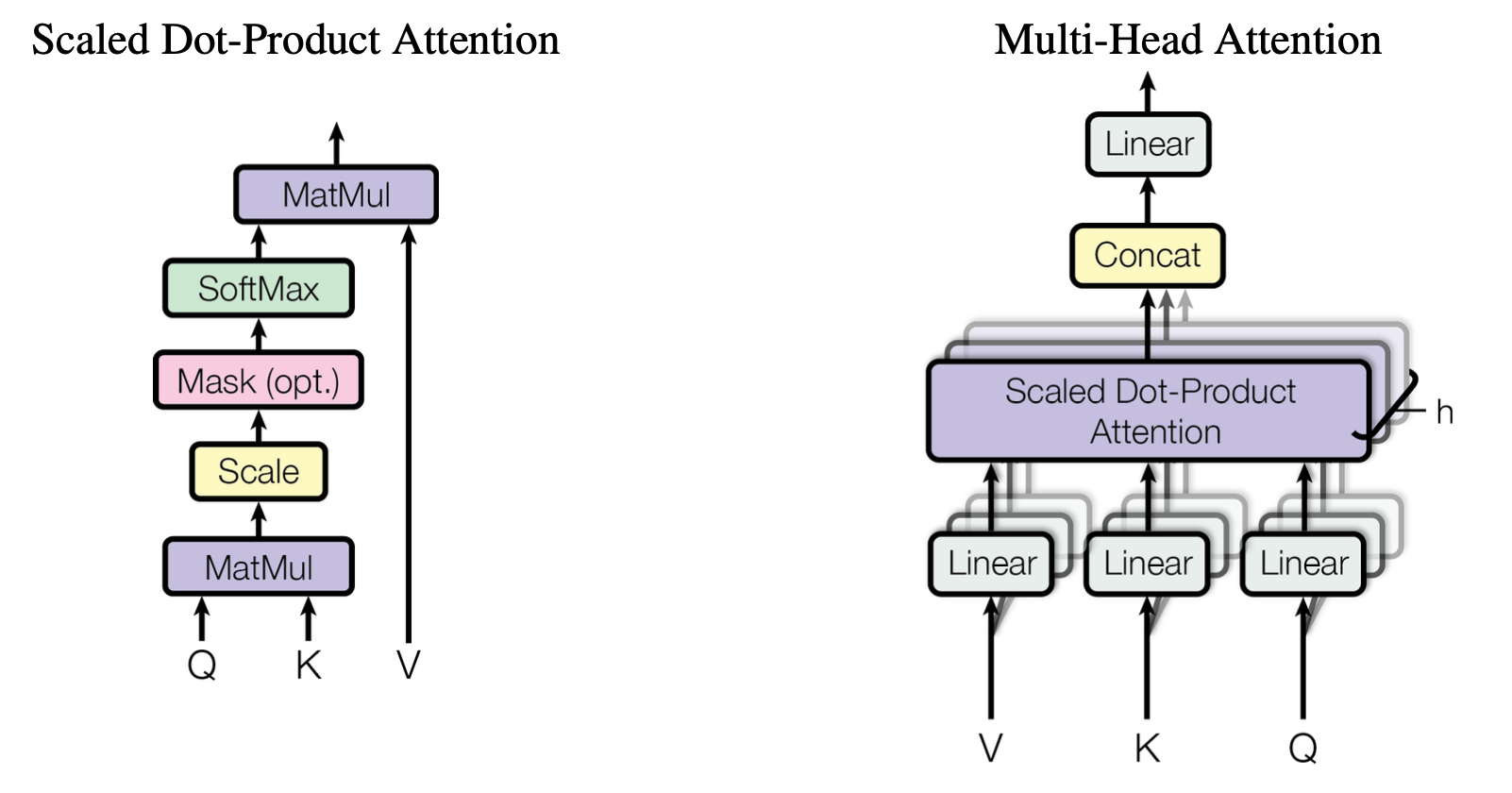
위 그림의 왼쪽은 Scaled Dot-Product Attention 메커니즘을 설명하는 그림이다. 입력은 \(d_k\)차원의 벡터들로 구성된 하나의 Query와 여러 Key들의 집합, 그리고 \(d_v\)차원의 벡터들로 구성된 여러 Value들의 집합이다. Query는 모든 Key들과 내적(Dot-Product)를 수행하고 그 결과물을 \(\sqrt{d_k}\)로 나눈 다음 Softmax 함수를 적용하여 가중치를 계산한다. 이렇게 계산된 가중치는 주어진 Query에 대한 전체 Key들 각각의 Attention 점수이다.
이 Attention 점수 계산 과정을 행렬 연산을 통해서 좀 더 간단히 쓸 수 있다. Query는 \(\mathbf{Q} \in \mathbb{R}^{L_q \times d_k}\), Key 집합은 \(\mathbf{K} \in \mathbb{R}^{L_k \times d_k}\), 그리고 Value 집합은 \(\mathbf{V} \in \mathbb{R}^{L_k \times d_v}\)라고 행렬 형태로 쓸 수 있다. 이 경우 Attention 함수는 다음과 같이 쓸 수 있다:
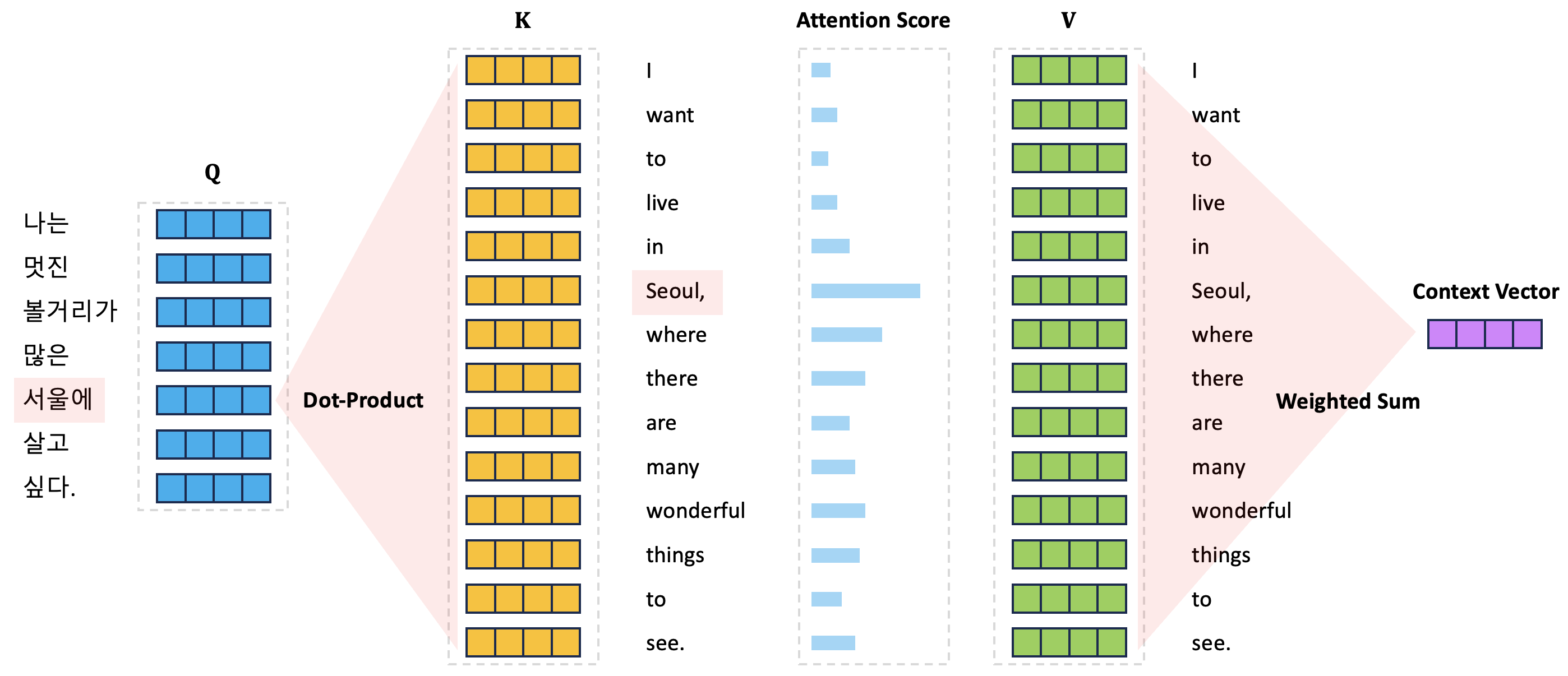
\[\text{Attention}\left( \mathbf{Q}, \mathbf{K}, \mathbf{V} \right) = \text{Softmax} \left( \frac{\mathbf{Q}\mathbf{K}^\text{T}}{\sqrt{d_k}} \right) \mathbf{V}.\]아래 그림은 Attention 함수가 어떤 방식으로 동작하는지를 설명하는 그림이다. 기본적으로 아래 그림의 상황은 입력 문장 “I want to live in Seoul, where there are many wonderful things to see.”을 한국어로 번역하는 과정에서의 Attention 함수 계산 과정을 나타낸다. 정답 문장의 각 토큰들의 임베딩 벡터는 Query 행렬의 행벡터로 구성되어 입력 문장 토큰 시퀀스에서 어느 토큰에 집중할지를 Attention 점수를 통해서 계산한다.
그림에서는 “서울에”라는 정답 문장의 토큰을 생성하는 과정에서 입력 문장 토큰들 각각의 Attention 점수가 Query 행렬의 “서울에” 토큰에 해당하는 행벡터와 입력 문장 토큰들 전체의 Key 벡터(Key 행렬의 행벡터로 구성되고 있음) 사이의 내적 계산을 통해서 구할 수 있다. 이렇게 구해진 입력 문장 토큰들 각각의 Attention 점수는 입력 문장 토큰들 각각의 Value 벡터(Value 행렬의 행벡터로 구성되고 있음)와 가중합을 계산하여 결과 문맥 벡터를 생성한다.
Multi-Head Attention
이러한 방식으로 Query, Key, Value에 대한 하나의 Attention 함수를 적용하는 대신 이를 \(h\)번 반복 수행하여 획득한 결과를 활용하는 Multi-Head Attention이 더욱 효과가 좋다는 것을 저자들은 주장한다. Multi-Head Attention이란 Query, Key, Value 각각을 \(h\)번에 걸쳐서 서로 다른 Attention을 수행하고 이 정보를 통합해서 활용하는 방법을 말한다.
Multi-Head Attention은 이를 위하여 Query, Key, Value 각각을 \(h\)번에 걸쳐서 선형 변환을 통해 학습된 새로운 공간으로 투영한다. 여기서 Query, Key, Value 각각을 투영한 공간의 차원은 \(d_k\), \(d_k\), \(d_v\)이다. 이렇게 투영된 \(h\)개의 벡터들을 통해서 Attention을 \(h\)번 수행는 것을 말한다.
즉, Attention Head가 여러개(여기서는 \(h\)개)가 있고 각각의 Head가 서로 다른 표현 보조 공간(Representation Subspace)로부터 서로 다른 Attention 정보를 추출하는 것을 동시에 학습할 수 있도록 하는 구조이다.
Multi-Head Attention은 모델로 하여금 Head가 서로 다른 Attention 정보를 획득할 수 있도록 하고 Single-Head의 경우에는 이 서로 다른 Attention 정보를 따로 획득하는 것이 아니라 이들을 모두 평균치를 내서 다루게 된다. Multi-Head Attention을 수식으로 설명하면 다음과 같다:
\[\begin{array}{rl} \text{MultiHead} \left( \mathbf{Q}, \mathbf{K}, \mathbf{V} \right) & = \text{Concat} \left( \text{head}_1, \text{head}_2, \cdots, \text{head}_h \right) \mathbf{W}^O, \\ \text{where} \ \text{head}_i & = \text{Attention} \left( \mathbf{Q}\mathbf{W}_i^Q, \mathbf{K}\mathbf{W}_i^K, \mathbf{V}\mathbf{W}_i^V \right). \end{array}\]여기서 Query, Key, Value 행렬의 차원은 아래와 같다:
\[\mathbf{Q} \in \mathbb{R}^{L_q \times d_\text{model}}, \mathbf{K} \in \mathbb{R}^{L_k \times d_\text{model}}, \mathbf{V} \in \mathbb{R}^{L_k \times d_\text{model}}.\]그리고 투영을 위한 파라미터 행렬들의 차원 역시 아래를 통해서 확인할 수 있다:
\[\mathbf{W}_i^Q \in \mathbb{R}^{d_\text{model} \times d_k}, \mathbf{W}_i^K \in \mathbb{R}^{d_\text{model} \times d_k}, \mathbf{W}_i^V \in \mathbb{R}^{d_\text{model} \times d_v}, \mathbf{W}^O \in \mathbb{R}^{ d_v \times d_\text{model}}.\]그렇다면 단순 Single-Head인 경우에 비해서 Multi-Head Attention의 효과는 어떤 것이 있을까? 우선 방금 위에서 Attention 함수가 동작하는 원리를 설명한 그림에서 확인할 수 있듯이 “서울에” 토큰을 생성할 때 입력 문장의 “Seoul,” 토큰에 더 집중하기 위한 Attention 점수의 Alignment 벡터가 계산된다. 이 결과는 문장의 통사론적(Syntactic), 의미론적(Semantic) 구조를 반영하여 “서울에”와 “Seoul,”을 연결하고 있는 결과라고 해석할 수 있다.
하지만 통사론적/의미론적 구조는 다양한 관점으로 해석이 가능하다. 이를 확인하기 위하여 아래의 예시들을 추가로 살펴보도록 하자.
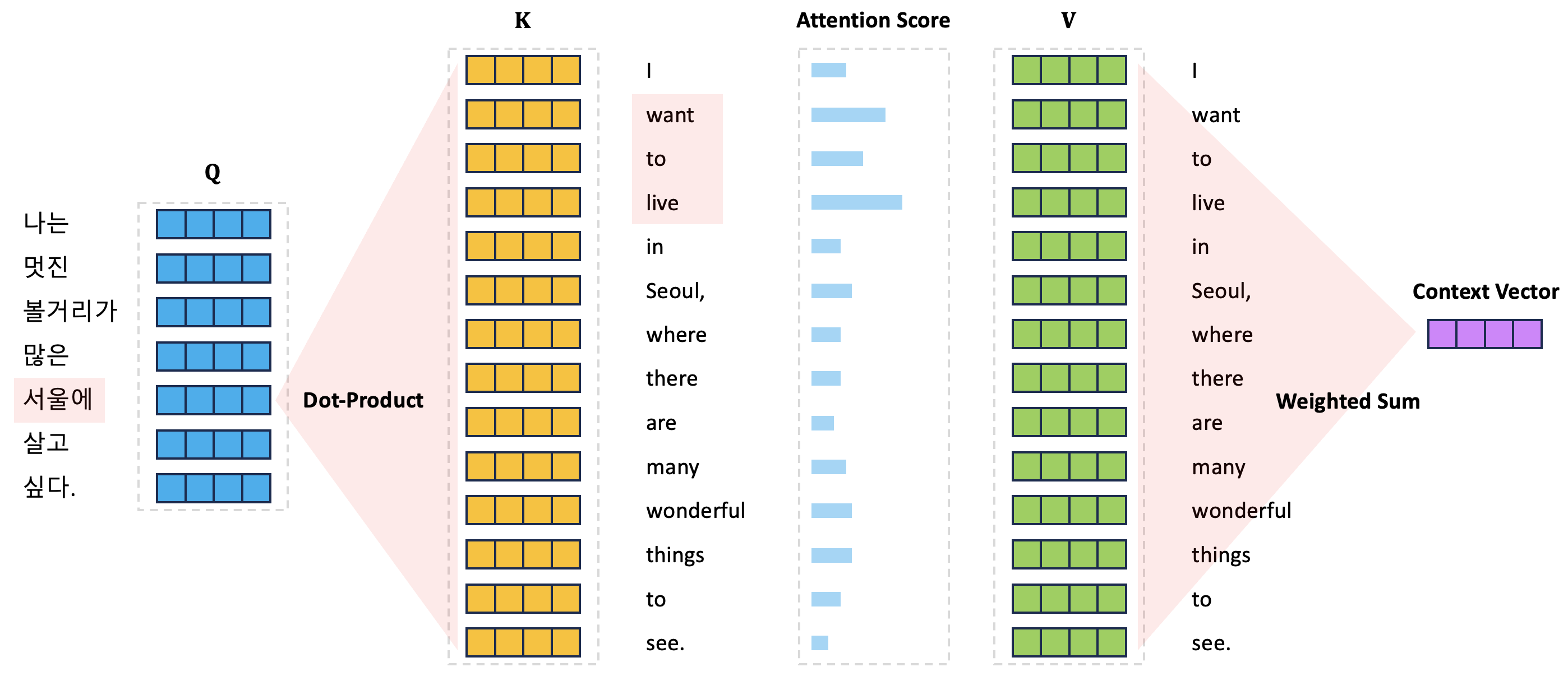
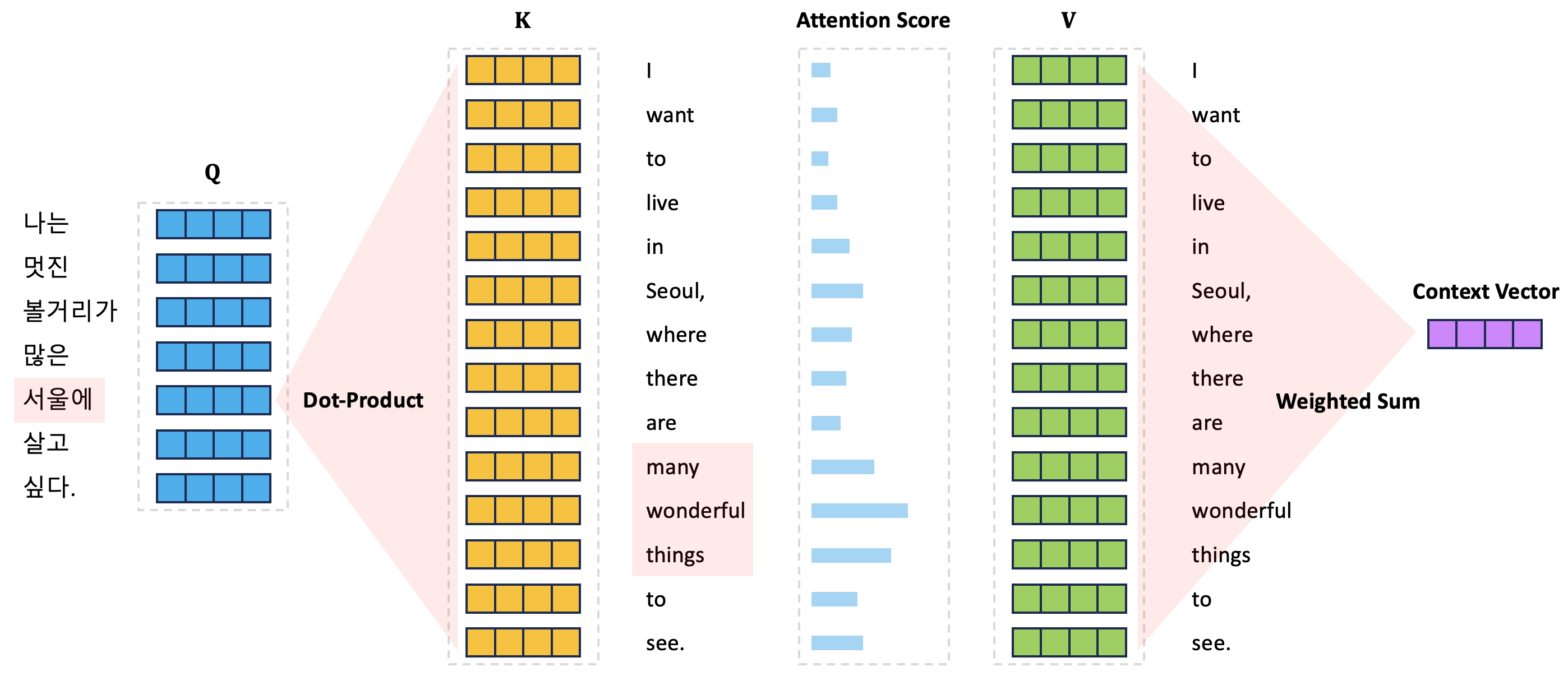
첫 번째 예시는 “서울에” 토큰을 생성하기 위하여 “want”, “to”, “live”라는 토큰들에 집중하고 있는 모습을 나타내고 있다. 이는 의미론적으로 서울이 내가 살고 싶은 곳이라는 의미를 반영하여 “서울에” 토큰과 “want”, “to”, “live” 토큰을 연결하고 있는 모습이다. 두 번째 예시는 “서울에” 토큰과 “many”, “wonderful”, “things” 토큰이 연결이 된 예시이다. 마찬가지로 서울에는 볼 것이 많다는 의미를 반영하여 해당 토큰들을 연결한 것을 확인할 수 있다.
즉, Multi-Head Attention은 Single-Head인 경우보다 좀 더 다양한 통사론적/의미론적 관점을 반영하여 Attention을 수행한다는 점에서 더욱 풍부한 문맥 벡터를 생성할 수 있다는 장점이 있다고 볼 수 있다.
위치별 완전 연결 순전파 망
Attention 보조 계층에 추가적으로 각각의 인코더와 디코더는 완전 연결 순전파 망을 보유하고 있다. 위에서 설명하였듯이 각각의 완전 연결 순전파 망은 동일한 가중치를 통해서 각 토큰의 위치별로 독립적이고 동일하게 적용된다. 이러한 이유로 위치별 완전 연결 순전파 망이라고 부르게 된다. 이 망은 두 개의 선형 변환과 그 사이에 ReLU 활성 함수로 구성되어 있다:
\[\text{FFN} = \max \left( 0, \mathbf{x} \mathbf{W}_1 + \mathbf{b}_1 \right) \mathbf{W}_2 + \mathbf{b}_2.\]임베딩과 Softmax
기존의 다른 시퀀스 변환 모델들과 동일하게 입력 토큰에 대한 임베딩 벡터화 과정을 Transformer도 포함하고 있다. 다른 모델들과 마찬가지로 임베딩 테이블은 훈련을 통해서 획득하거나 또는 이미 훈련된 임베딩 테이블을 가져와서 파인 튜닝(Fine-Tuning)을 수행한다. 기본적으로 입력 임베딩 벡터의 차원은 \(d_\text{model}\)이다. 또한 디코더의 출력에는 다음 토큰의 확률을 추론하기 위해서 선형 변환 및 그 변환 결과에 대한 Softmax 함수 처리를 수행한다.
Transformer는 특이하게도 이 논문에서 주장한 바와 동일하게끔 입력 임베딩의 가중치와 출력 임베딩, 즉 출력 Softmax 들어가기 바로 전의 선형 변환의 가중치를 동일하게 설정하였다.
위치 인코딩
Transformer 모델은 분명 순서가 있는 시퀀스 데이터를 다루지만 Recurrence나 Convolution을 수행하지 않는 구조이기 때문에 이러한 데이터의 순서 정보를 인코딩할 수 있는 다른 방법이 필요하다. Transformer 모델은 위치 인코딩(Positional Encoding)이라는 방법을 활용하여 이 문제를 해결한다. 위치 인코딩은 기본적으로 현재 위치에 대한 순서 정보를 입력 임베딩 벡터와 동일한 크기인 \(d_\text{model}\)로 설정한다. 이를 통해서 입력 임베딩과 위치 인코딩은 서로 더해질 수 있게 된다. 이렇게 더해진 벡터는 인코더와 디코더의 입력으로 활용되게 된다.
Transformer 모델에서 활용한 위치 인코딩 방법은 사인 함수와 코사인 함수를 활용하여 다음과 같이 표현된다:
\[\begin{array}{rl} PE_{(pos, 2i)} & = \sin \left( \left( \frac{pos}{10000} \right)^{\frac{2i}{d_\text{model}}} \right), \\ PE_{(pos, 2i + 1)} & = \cos \left( \left( \frac{pos}{10000} \right)^{\frac{2i}{d_\text{model}}} \right). \end{array}\]여기서 \(pos\)는 위치 정보이고 \(2i\)와 \(2i + 1\)은 차원이다. 즉 위치 인코딩의 각 차원은 모두 사인파 형태의 파동으로 구성되어 있는 것이다. 이 파동의 파장은 \(i\)가 증가함에 따라서 \(2\pi\)에서 \(20000\pi\)가 될 것이다. 각각의 차원에 따라서 파형이 달라지고 그 파형을 위치별로 따라가는 형태로 위치 인코딩이 수행된다. 이러한 형태의 위치 인코딩 방식을 선택한 이유를 저자들은 모델이 상대적인 위치에 집중할 수 있도록 하기 때문이라고 한다.
위치 인코딩을 위치 자체에 대한 학습 가능한 임베딩 테이블을 구성하여 학습시키는 방식을 구상하기도 하였다. 저자들은 실험 결과 사인 함수, 코사인 함수를 활용한 위치 인코딩과 위치 임베딩 방식의 성능차가 거의 없었다고 말한다. 사인 함수, 코사인 함수를 활용하면 파라미터의 수가 더 줄어들기 때문에 아마도 이를 선택하였던 것 같다.
Self-Attention을 통한 이점
가변 길이의 심벌 표현 시퀀스 \(\left( \mathbf{x}_1, \cdots, \mathbf{x}_n \right)\)을 인코더-디코더 구조에서 은닉 벡터 등의 같은 길이의 시퀀스 \(\left( \mathbf{z}_1, \cdots, \mathbf{z}_n \right)\)로 변환하는 변환 태스크에서 Transformer 모델의 Self-Attention 메커니즘은 기존의 다른 방식의 방법론들, 예를 들면 Recurrent와 Convolution 등와 방법론들에 비해서 몇 가지 이점을 가지고 있다.
먼저 계산 복잡도에서 이점을 가지고 있다. Self-Attention 메커니즘은 병렬적으로 동시에 진행될 수 있는 계산 방식을 보유하고 있어서 총 계산 복잡도에서 시간적인 이점을 가지고 있다. 그 다음은 Long Term Dependency를 잘 학습할 수 있다는 점이다. 좀 더 구체적으로는 Long Term Dependency를 위한 경로가 기존 방법들에 비해서 짧아서 신경망 내부의 순전파와 역전파의 신호가 전달되는 길이가 훨씬 짧다. 이는 Vanishing Gradient 문제를 줄여주며 Long Term Dependency를 더욱 잘 학습할 수 있도록 도와준다.
| 계층 타입 | 계층별 복잡도 | 시퀀스 연산수 | 최대 경로 길이 |
|---|---|---|---|
| Self-Attention | \(O(n^2 \cdot d)\) | \(O(1)\) | \(O(1)\) |
| Recurrent | \(O(n \cdot d^2)\) | \(O(n)\) | \(O(n)\) |
| Convolution | \(O(k \cdot n \cdot d^2)\) | \(O(1)\) | \(O(\log_kn)\) |
| Self-Attention (Restricted) | \(O(r \cdot n \cdot d)\) | \(O(1)\) | \(O\left( \frac{n}{r} \right)\) |
위의 표는 각 계층 타입별 계산 복잡도를 정리한 것이다. Self-Attention은 모든 위치에 동시에 연결되어 있으며 이는 시퀀스 연산이 특정 상수 횟수 이내에 계산될 수 있다는 의미이다. 따라서 시퀀스 연산수는 \(O(1)\)이다. 반면 Recurrent 모델은 위치에 따라서 순서대로 계산되기 때문에 시퀀스 연산수가 \(O(n)\)이 된다. 여기서 \(n\)은 시퀀스 길이이다.
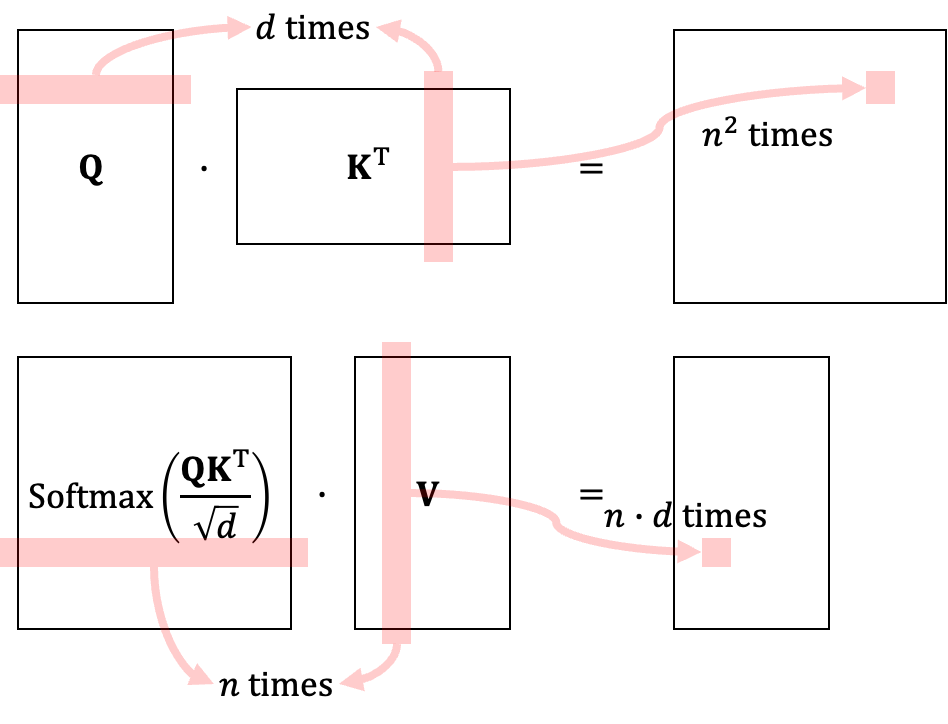
위 그림은 Transformer의 Self-Attention 모델에 대한 계층별 복잡도를 설명하기 위한 그림이다. 행렬 \(\mathbf{Q}\)와 \(\mathbf{V}\)를 곱하기 위해서 필요한 계산량은 결과 행렬의 크기인 \(n^2\)에다가 각 요소를 구하기 위해 필요한 계산량 \(d\)를 곱하여 \(n^2 \cdot d\)가 된다. 그 다음으로 \(\text{Softmax} \left( \frac{\mathbf{QV}^\text{T}}{\sqrt{d}} \right)\)와 \(\mathbf{V}\)를 곱하기 위해서는 결과 행렬의 크기인 \(n \cdot d\)와 더불어 각 성분을 계산하기 위해서 필요한 \(L\)을 곱하여 마찬가지로 \(n \cdot d\)가 된다. 따라서 Transformer의 계층별 복잡도는 \(n^2 \cdot d + n^2 \cdot d = O(n^2 \cdot d)\)가 된다.
반면 Recurrent 모델은 \(d\)차원으로부터 \(d\)차원으로의 선형 변환으로 구성되어 있으며 따라서 전체 시퀀스 길이 \(n\)에 \(d^2\)만큼의 계산량을 곱한 \(n \cdot d^2\)만큼의 계층별 계산량을 보유하고 있다. 따라서 만약 시퀀스 길이 \(n\)이 \(d\)보다 매우 큰 상황이라면(보통은 이런 상황이 일반적이다.) 계층별 복잡도는 Recurrent에 비해서 Self-Attention 모델이 훨씬 더 높을 것이다. 대신 시퀀스 연산수는 Self-Attention 모델이 상수임에 반해 Recurrent 모델의 시퀀스 연산수는 \(O(n)\)이므로 시간적으로는 Self-Attention 모델이 훨씬 좋다. 결론적으로 말하면 추론 속도는 Self-Attention 모델이 더 좋겠지만 전체 계산 복잡도는 Recurrent 모델이 더 좋은 것이다.
이러한 계층별 복잡도 문제를 줄이기 위해서 Self-Attention 모델을 약간 제한을 걸어서 계산 복잡도를 줄이는 방법이 있다. \(n\)개의 전체 시퀀스를 바라보는 것이 아닌 근처에 있는 \(r\)개 만을 바라보는 것이다. 이를 통해서 계층별 복잡도를 \(O(r \cdot n \cdot d)\)로 줄일 수 있다. 이는 위의 표에서 Self-Attention (Restricted)로 정의되어 있다.
추가적으로 저자들은 Self-Attention 모델은 좀 더 해석가능한 모델이라고 주장한다. 실험적으로 Transformer 모델은 문장의 통사론적/의미론적 구조를 잘 찾아내고 있음을 확인할 수 있다.
기계 번역 결과 분석
Transformer 모델은 기계 분석 태스크에서 기존의 다른 모델들에 비해서 좋은 성능을 보이는 것을 확인할 수 있다. 기계 번역 태스크에서의 Metric은 BLEU 점수라는 것인데 Transformer 모델은 대부분의 모델들에 비해서 더 높은 BLEU 점수를 획득했다. BLEU 점수에 대한 이야기는 나중에 다뤄보도록 하겠다. 또한 추가적으로 기존의 다른 모델들에 비해서 Transformer 모델의 훈련 비용은 훨씬 더 저렴했다.
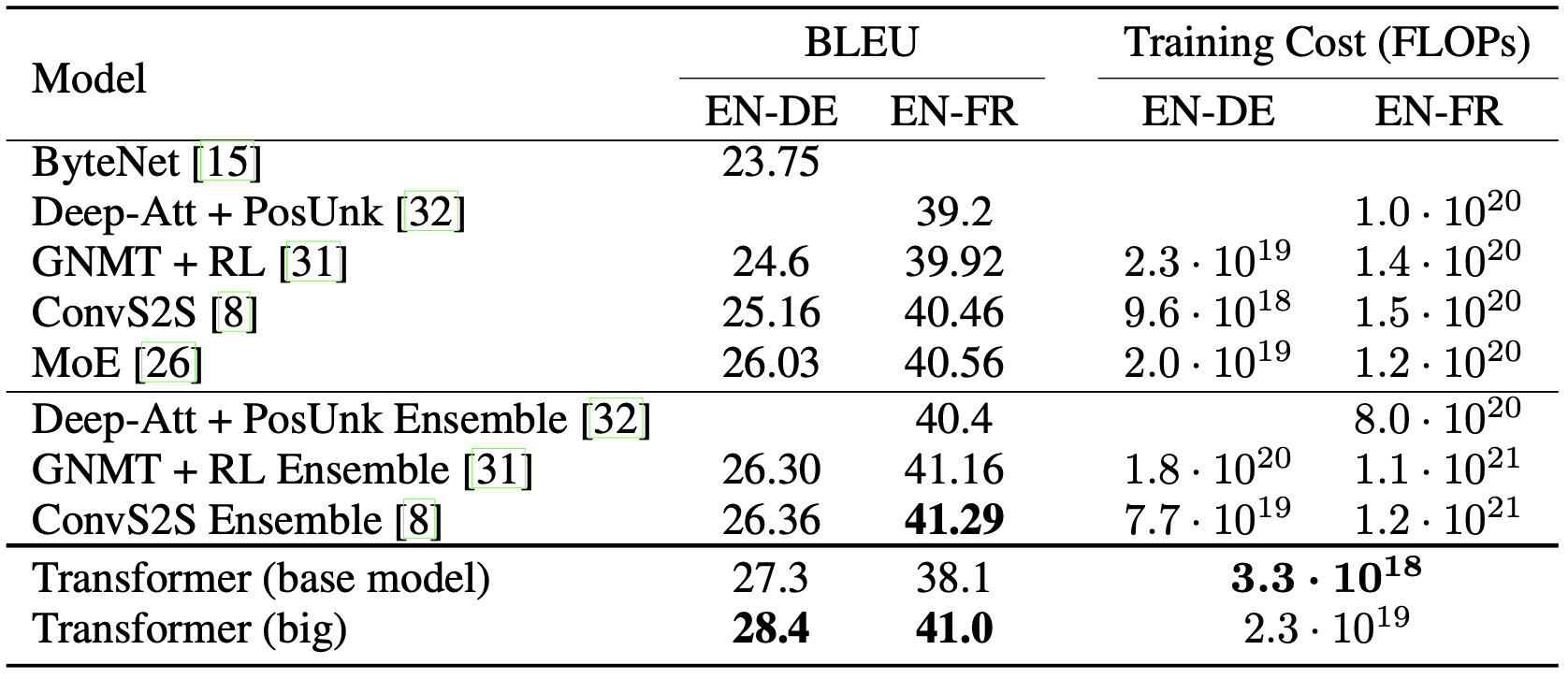
위 표는 논문에서 가져온 Transformer 모델과 기존 다른 모델들 사이의 성능과 훈련 비용에 대한 비교를 나타낸다. 태스크는 영어와 독일어 사이의 번역을 수행하는 태스크인 WMT 2014 태스크를 수행했다.
정리
본 포스트에서는 Transformer를 소개하는 내용을 다뤄보았다. Transformer는 기존의 기계 번역 태스크와 같은 Sequence-to-Sequence 모델에서 흔히 겪을 수 있는 Long Term Dependency 문제를 해결할 수 있었고 또한 시퀀스 연산 복잡도를 \(O(n)\)에서 \(O(1)\)으로 낮출 수 있었다.
또한 Transformer는 추가적으로 Multi-Head Attention을 통해서 단순히 하나의 Attention을 통해서만 얻을 수 있는 통사론적/의미론적 Attention 점수만을 활용하는 것이 아니라 여러 관점에서의 Attention 점수를 활용할 수 있는 구조를 가지고 있다. 이를 통해서 획득한 문맥 벡터에 담긴 정보를 더욱 풍부하게 만들 수 있었다.
Transformer의 이러한 문맥 정보를 잘 찾아낼 수 있는 장점들은 향후 거대 언어 모델의 뼈대가 되는 중요한 모델로 Transformer가 선택되는 결과를 만들게 된다. 이후 거대 언어 모델들을 다룰때 Transformer는 계속해서 등장할 예정이니 꼭 숙지해야 할 것이다.
참고 자료
수정 사항
- 2023.02.25
- 최초 게제
- 2023.02.27
- Attention 메커니즘 내용 정리
- 2023.03.02
- Transformer 내용 정리
- 2023.11.19
- 목차 추가
- 2023.11.23
- Attention 메커니즘 내용 보충
- 최종 정리 추가
- 2023.11.26
- Attention 메커니즘 내용 보충
- Transformer 내용 보충
- 2023.12.3
- Attention 메커니즘 내용 및 예시 보충