이번 포스팅은 다음의 논문을 스터디하여 정리하였다:
또한 TensorFlow 공식 홈페이지를 참고하여 작성하였다.
Stochastic Gradient Descent
딥러닝을 학습하는 알고리즘으로 가장 일반적으로 많이 쓰이는 방법은 바로 Stochastic Gradient Descent (SGD)이다. SGD를 설명하기 전 Gradient Descent를 먼저 간단하게 설명하면 파라미터 \(\theta\)에 대해서 정의된 특정 Cost \(L(\theta)\)를 최적화하기 위하여 \(L(\theta)\)의 Gradient를 이용하는 방법이다. \(L\)의 Gradient는 파라미터 \(\theta\) 스페이스 상에서 \(L\)을 최대화하는 방향의 벡터값을 갖게 되므로 여기에 Learning rate \(\alpha\)를 곱해서 현재 파라미터 \(\theta\)에서 빼주면 현재 Cost \(L\)이 감소하는 방향으로 파라미터 \(\theta\)를 업데이트할 수 있게 된다.
즉, 업데이트 룰은 다음과 같다.
\[\theta_{k+1} = \theta_k - \alpha \nabla_{\theta} L(\theta) |_{\theta=\theta_k}\]이러한 업데이트를 통하여 다음의 최적화 문제를 풀 수 있게 된다.
\[\theta = \arg \min_\theta L(\theta)\]Data-driven 방식을 통하여 Gradient Descent를 사용하기 위해서는 주어진 트레이닝용 데이터에 대한 Cost를 정의하여 그 Cost를 최소화하기 위한 \(\theta\)를 찾아내야 한다. 즉, 주어진 데이터셋 \(D\)에 대한 최적화 문제는 다음과 같다.
\[\theta = \arg \min_\theta L(x, \theta), \forall x \in D\]이러한 최적화 문제를 풀기 위한 Gradient Descent 업데이트 룰 또한 다음과 같이 정의할 수 있을 것이다.
\[\theta_{k+1} = \theta_k - \alpha \mathbb{E}_{x\in D} [ \nabla_{\theta} L(x, \theta) |_{\theta=\theta_k} ]\]실제로 이 룰을 활용하는 경우에는 모든 데이터셋 \(D\)를 전부 활용하기 힘든 여러가지 이유들로 인하여 미니배치를 반복적으로 샘플링하여 업데이트하는 방법인 Stochastic Gradient Descent를 사용한다. 미니배치의 크기를 \(N\)이라고 했을 때, 실제 Gradient를 다음과 같은 Stochastic Gradient로 근사화를 할 수 있다.
\[\mathbb{E}_{x\in D}[ \nabla_\theta L(x, \theta) ] \approx \frac{1}{N} \sum_{i=1}^N \nabla_\theta L(x_i, \theta)\]물론 이러한 SGD같은 방법에도 ADAM, Adagrad 등의 여러 베리에이션이 존재하지만 그 내용들은 다음에 다루도록 하고 여기서는 이정도만 정리하고 넘어가도록 하겠다. 어쨌든 Batch Normalization 논문에서는 SGD가 다음과 같은 특징들이 있다고 정리하고 있다.
- Stochastic Gradient는 실제 Gradient의 추정값이며 이것은 미니배치의 크기 \(N\)이 커질수록 더 정확한 추정값을 가지게 된다.
- 미니배치를 뽑아서 연산을 수행하기 때문에 최신 컴퓨팅 플랫폼에 의하여 병렬적인 연산 수행이 가능하여 더욱 효율적이다.
SGD의 문제점
SGD의 문제점이라지만 사실 딥 뉴럴넷의 문제점이라고 보는 것이 맞을 듯 싶다. 논문에서는 레이어를 여러 층으로 쌓음으로써 생기는 문제점들에 대해서 얘기하고 있다. 어쨌든 논문에서 얘기하는 SGD의 문제점은 뉴럴넷을 학습하기 위한 하이퍼 파라미터들의 초기값 설정을 굉장히 신중하게 해줘야만 한다는 점이다. 이전 네트워크에서의 파라미터 변화는 그 다음, 그 다음 네트워크들을 거치며 점점 변화량이 증폭된다. 따라서 신중하지 못한 파라미터 초기화의 문제점은 레이어가 쌓이면서 더욱 큰 문제로 발전하게 될 것이다.
뉴럴넷의 입력 분포의 변화가 일어난다면 뉴럴넷의 각 레이어들은 그 새로운 분포에 끊임없이 적응해야하는 문제가 있다. 이 경우에 뉴럴넷은 Covariate Shift를 겪었다고 말한다.
다음과 같은 뉴럴넷 연산을 살펴보자.
\[l = F_2(F_1(u, \theta_1), \theta_2)\]\(F_1\), \(F_2\)는 임의의 Transformation이고, 파라미터 \(\theta_1\), \(\theta_2\)는 Loss \(l\)을 최소화하는 방향으로 학습이 진행된다.
여기서 하위 네트워크 \(F_2\)의 파라미터 \(\theta_2\)는 다음과 같은 방식으로 학습이 된다고 볼 수 있다.
\[\theta_2 \leftarrow \theta_2 - \frac{\alpha}{m}\sum_{i=1}^m \nabla_{\theta_2}F_2(x_i, \theta_2)\]이건 마치 \(F_2(x, \theta_2)\)를 단독으로 학습하는 것과 동일하다. 따라서 학습을 더 원할하게 만들어주는 입력 분포는 모델을 구성하는 하위 네트워크들에 대해서도 동일하게 적용된다고 볼 수 있다!
여기까지 나온 개념을 일단 정리해 보자면:
- 뉴럴넷의 입력 분포 변화는 일어나지 않는 것이 좋다! 왜? 뉴럴넷 파라미터들이 그 분포에 새로 적응해야 하기 때문!
- 즉, 학습을 원할하게 하기 위해 효율적인 입력 분포는 일정하게 유지되는 입력 분포
- 네트워크를 여러 층을 쌓은 경우에 하위 네트워크에 대한 입력 분포의 효율성에도 동일하게 적용된다!
- 즉, 앞단의 레이어의 출력(다시말해 뒷단의 레이어의 입력이 될 값)의 분포도 일정하게 유지하는 것이 좋음!
논문에서 언급하고있는 또 다른 문제점은 Gradient Descent 및 뉴럴넷의 Nonlinearity에 의한 Saturated Regime에 관한 문제이다. 일반적으로 뉴럴넷의 Activation은 Sigmoid를 사용하는데 이 Sigmoid의 특성상 절대값이 일정 수준 이상으로 큰 입력에 대해서는 Gradient가 거의 사라지는 문제가 발생한다.
즉, 다음의 뉴럴넷 구조를 살펴보자.
\[z = g(Wu + b)\]여기서 g는 다음과 같은 Sigmoid 함수이다.
\[g = \frac{1}{1 + e^{-x}}\]이때 Sigmoid 함수의 특성상 입력 \(x\)의 절대값의 크기가 커질수록, 즉 \(0\)으로부터 멀어질수록 Gradient 값이 매우 작아지게 된다. 따라서 \(0\) 근방이 아닌 입력들에 대해서는 잘 학습이 되지 않을 것이며 만약 \(x\)의 분포가 \(0\)으로부터 멀어진다면 더이상 학습이 진행이 되지 않고 모델은 특정 파라미터 값에서 Saturation이 되게 될 것이다. 이 현상을 Saturated Regime에 빠졌다고 하는 것 같다. Saturated Regime에 대해서는 좀 더 조사해보고 정리하도록 하겠다
어쨌든 이러한 이유들이 뉴럴넷 모델의 각 레이어들의 입력들의 분포를 일정하게 유지시켜주는 것이 왜 필요한지에 대한 설명이 될 것 같다.
Covariate Shift를 줄이기 위한 시도
먼저 Internal Covariate Shift에 대한 정의를 하고 넘어가도록 하자.
- Internal Covariate Shift의 정의: 네트워크의 학습 도중에 파라미터의 변화로 인한 네트워크 Activation(출력)들의 분포 변화
학습 효율을 높이기 위해서는 이런 Internal Covariate Shift를 줄이기 위한 노력이 필요하다. 기존의 여러 연구 결과들은 입력값들이 Whitening된다면, 즉, Zero Mean과 Unit Variance를 가지게 되고 각각의 입력값들이 Decorrelated된다면, 뉴럴넷이 훨씬 빠르게 수렴할 것이라고 말하고 있다. 또한 모든 레이어들이 같은 Whitening 방식을 공유한다면 훨씬 이득을 가질 수 있다고 한다.
기존의 연구에서는 뉴럴넷의 파라미터를 Activation의 값에 따라서 바꾸면서 Whitening하는 방식을 사용하였다. 하지만 이러한 방법은 Gradient Descent Step의 효과를 줄이는 결과를 가져온다.
예를 들면, 입력값 \(u\)에 학습된 바이어스 \(b\)를 더해주고 트레이닝용 데이터의 Activation의 Mean을 빼주는 방식으로 Normalization을 수행하는 레이어를 생각해보자.
\[\widehat{x} = x - \mathbb{E}[x], \ \text{where} \ x = u + b, \mathcal{X}=\{x_1,\cdots, x_N\}\]만약 Gradient Descent Step이 $\mathbb{E}[x]$와 \(b\)의 Dependency를 무시하고 수행된다면 다음과 같은 업데이트 룰을 따르게 된다.
\[b \leftarrow b + \Delta b, \ \text{where} \ \Delta b \propto -\frac{\partial l}{\partial \widehat{x}}\]이러한 업데이트 룰을 따르게 된다면 다음과 같은 결과를 확인할 수 있다.
\[u + (b + \Delta b) - \mathbb{E}[u + (b + \Delta b)] = u + b - \mathbb{E}[u + b]\]즉, 업데이트 전후의 Normalization 결과 \(\widehat{x}\)가 같게 되며 결과적으로 Loss \(l\)의 값 역시 일정하게 유지된다. \(\widehat{x}\), \(l\)의 변화가 없게 된다면 Gradient \(\Delta b\)의 값이 불분명하게 되고 이것은 업데이트가 제대로 되지 않는 결과를 가져오게 된다. 이러한 현상은 단순히 Zero Mean을 위한 Centering 뿐 아니라 Unit Variance를 위한 Scaling에서도 마찬가지로 발생되게 된다. 따라서 이러한 방식의 Normalization은 문제가 된다!
위의 현상을 다음과 같이 설명할 수 있다. 먼저 Normalization을 다음과 같이 표현해보자.
\[\widehat{x} = \text{Norm}(x, \mathcal{X})\]따라서 이 Normalization 레이어의 Backpropagation을 구하려면 다음의 Jacobian을 구해야 한다.
\[\frac{\partial \text{Norm}(x, \mathcal{X})}{\partial x}, \ \text{and} \ \frac{\partial \text{Norm}(x, \mathcal{X})}{\partial \mathcal{X}}\]만약 \(\mathbb{E}[x]\)와 \(b\)의 Dependency를 무시한다는 것은 즉 뒤의 Term인 \(\frac{\partial \text{Norm}(x, \mathcal{X})}{\partial \mathcal{X}}\)을 무시한다는 것이다. 즉, \(\widehat{x}\)은 엄밀하게는 다음과 같이 표현해야 한다.
\[\widehat{x} = \text{Norm}(x, \mathcal{X}) = x - \mathbb{E}_{x \in \mathcal{X}}[x], \ \text{where} \ x = u + b, \mathcal{X}=\{x_1,\cdots, x_N\}\]추가적으로 이러한 방식의 Whitening은 Covariance를 구해야 한다는 이유로 인하여 연산이 매우 복잡하다는 단점이 있다. Covarialce Matrix를 구하려면 다음의 연산을 수행하여야 한다.
\[\text{Cov}[x] = \mathbb{E}_{x\in \mathcal{X}}[xx^T] - \mathbb{E}[x]\mathbb{E}[x]^T\] \[\text{Cov}[x]^{-1/2}(x-\mathbb{E}[x])\]뿐만아니라 이것들의 Backpropagation까지 구해야 한다!
따라서 Batch Normalization의 저자들은 여기에서 동기를 얻어서 파라미터 업데이트 이후마다의 트레이닝 셋 전체의 분석이 필요하지 않을 뿐 아니라 미분도 가능해서 Backpropagation을 구하는 것이 용이한 어떤 입력 Normalization을 찾는 연구를 시도했다고 한다.
Batch Normalization: 미니배치의 Statistics를 이용
Batch Normalization은 각각의 스칼라 Feature들을 독립적으로 정규화하는 방식으로 진행된다. 즉, 각각의 Feature들의 Mean 및 Variance를 \(0\)과 \(1\)로 정규화를 하는 것이다. 정규화를 위해서는 \(d\) 차원의 입력 \(x=(x^{(1)}, \cdots, x^{(d)})\)에 대해서 다음의 연산을 수행해야 한다.
\[\widehat{x}^{(k)} = \frac{x^{(k)} - \mathbb{E}[x^{(k)}]}{\sqrt{\text{Var}[x^{(k)}]}}\]근데 위에서 설명하였듯이 저런식으로 하면 문제가 발생한다. 따라서 여기서는 각각의 Activation \(x^{(k)}\)에 대해서 새로운 파라미터 쌍 \(\gamma^{(k)}, \beta^{(k)}\)을 도입하여 이 문제를 해결한다.
\[y^{(k)} = \gamma^{(k)}\widehat{x}^{(k)} + \beta^{(k)}\]이 파라미터 \(\gamma^{(k)}\)와 \(\beta^{(k)}\)는 모델이 학습되어감에 따라 함께 학습이 이루어지며 이 파라미터의 역할은 본래 모델의 Representation Power을 유지시키는 역할을 하며 이 Representation Power 덕분에 위에서 언급했었던 단순 정규화의 문제점이 해결이 된다. 만약 다음과 같이 세팅을 할 수 있다면(Optimal하게 학습이 이루어졌다고 가졍한다면) \(y^{(k)}\)는 결국 원래의 Activation인 \(x^{(k)}\)가 복원된 결과가 될 것이다.
\[\gamma^{(k)} = \sqrt{\text{Var}[x^{(k)}]}, \ \ \ \beta^{(k)} = \mathbb{E}[x^{(k)}]\]또한 Batch Normalization의 또 다른 특징은 바로 미니배치 단위에서 정규화가 수행된다는 점이다. 모든 트레이닝 셋을 다 정규화에 활용할 수 있으면 좋겠지만 효율성을 위해서 미니배치를 Stochastic하게 샘플링하여 정규화를 수행하게 된다. 각각의 미니배치는 각각의 Activation에 대하여 Mean 및 Variance를 추정하는데 사용된다. 이러한 방식을 통해서 정규화에 사용되는 Statistics가 Backpropagation에 활용될 수 있게 된다.
여기서 눈여겨 봐야할 점은 미니배치 정규화는 각 차원들의 Activation들 각각에 대해서 수행되는 Per-dimension Variance를 계산하게 된다는 점이다. 즉, 각 차원들의 Activation들을 독립적이라고 가정하고 각각의 Activation들 사이의 Joint Covariance를 고려하지 않는다는 의미이다. 만약 Joint Covariance를 계산하게 되는 경우에는 미니배치 사이즈가 Activation들의 개수보다 작다는 일반적인 사실에 의하여 Singular Covariance Matrix가 생성되는 결과를 가져올 수 있다.
지금까지 설명한 Batch Normalization의 특징들을 정리하면 다음과 같다.
- 트레이닝을 위한 미니배치 단위에서 수행
- 미니배치 내의 한 Example 내에서의 Activation들은 각각 독립적이라고 가정
- 독립적인 각각의 Activation들은 정규화를 위하여 미니배치 내의 Example들의 Statistics를 이용
Batch Normalization 레이어의 트레이닝
Batch Normalization을 다음과 같이 정의하자. 미니배치 사이즈 \(m\)에 대한 미니배치 \(\mathcal{B}\)를 \(\mathcal{B}=\{x_1,\cdots, x_m\}\)과 같이 정의한다면 아래의 표현을 Batch Normalization 레이어의 연산으로 정의한다.
\[\text{BN}_{\gamma, \beta}: x_1,\cdots, x_m \rightarrow y_1,\cdots, y_m\]Batch Normalization 레이어의 학습 과정은 다음과 같다.
- 입력: 미니배치 \(\mathcal{B}\), 학습될 파라미터 \(\gamma, \beta\)
- 출력: \(\{y_i = \text{BN}_{\gamma, \beta}(x_i) \}\)
학습 과정에 대해서 좀 더 간단하게 정리하면 먼저 각 Activation의 Mean과 Variance를 미니배치 내에서 추정을 하여 Activation들을 각각 정규화를 시킨 다음에 파라미터 \(\gamma, \beta\)로 Scale 및 Shift를 수행하여 출력값을 내보내게 된다. 이 때 \(\gamma, \beta\)는 Backpropagation을 통해서 학습이 된다. 논문에 정리된 Backpropagation은 다음과 같다.
\[\begin{align*} \frac{\partial l}{\partial \widehat{x}_i} & = \frac{\partial l}{\partial y_i} \cdot \gamma \\ \frac{\partial l}{\partial \sigma_{\mathcal{B}}^2} & = \sum_{i=1}^m \frac{\partial l}{\partial \widehat{x}_i} \cdot (x_i - \mu_{\mathcal{B}}) \cdot \frac{-1}{2} \cdot \left( \sigma_{\mathcal{B}}^2 + \epsilon \right)^{-3/2} \\ \frac{\partial l}{\partial \mu_{\mathcal{B}}} & = \left( \sum_{i=1}^m \frac{\partial l}{\partial \widehat{x}_i} \cdot \frac{-1}{\sqrt{\sigma_{\mathcal{B}}^2 + \epsilon}} \right) + \frac{\partial l}{\partial \sigma_{\mathcal{B}}^2} \cdot \frac{\sum_{i=1}^m -2(x_i - \mu_{\mathcal{B}})}{m} \\ \frac{\partial l}{\partial x_i} & = \frac{\partial l}{\partial \widehat{x}_i} \cdot \frac{1}{\sqrt{\sigma_{\mathcal{B}}^2 + \epsilon}} + \frac{\partial l}{\partial \sigma_{\mathcal{B}}^2} \cdot \frac{2(x_i - \mu_{\mathcal{B}})}{m} + \frac{\partial l}{\partial \mu_{\mathcal{B}}} \cdot \frac{1}{m} \\ \frac{\partial l}{\partial \gamma} & = \sum_{i=1}^m \frac{\partial l}{\partial y_i} \cdot \widehat{x}_i \\ \frac{\partial l}{\partial \beta} & = \sum_{i=1}^m \frac{\partial l}{\partial y_i} \end{align*}\]Batch Normalization 레이어의 인퍼런스
인퍼런스는 트레이닝과 과정이 조금 다르다. 트레이닝에서는 Activation의 정규화 과정에서 미니배치와의 Dependency를 고려하지만 인퍼런스에서도 이렇게 된다면 미니배치의 세팅에 따라서 결과가 달라지게 된다. 따라서 인퍼런스에서는 결과를 Deterministic하게 하기 위하여 고정된 Mean과 Variance를 이용하여 정규화를 한다.
따라서 인퍼런스 전, 즉 트레이닝 과정에서 미리 미니배치를 뽑을 때 Sample Mean \(\mu_{\mathcal{B}}\) 및 Sample Variance \(\sigma_{\mathcal{B}}^2\)를 이용하여 각각의 Moving Average \(\mathbb{E}_{\mathcal{B}}[\mu_{\mathcal{B}}], \mathbb{E}_{\mathcal{B}}[\sigma_{\mathcal{B}}^2]\)를 구해놨어야 한다.
Moving Average를 이용하여 실제 Mean 및 Variance를 추정하면 다음과 같다.
\[\begin{align*} \mathbb{E}[x] & \leftarrow \mathbb{E}_{\mathcal{B}}[\mu_{\mathcal{B}}] \\ \text{Var}[x] & \leftarrow \frac{m}{m-1} \cdot \mathbb{E}_{\mathcal{B}}[\sigma_{\mathcal{B}}^2] \end{align*}\]이것을 이용하여 다음과 같이 인퍼런스를 수행한다.
\[\begin{align*} \widehat{x}_i & \leftarrow \frac{x_i - \mathbb{E}[x]}{\sqrt{\text{Var}[x] + \epsilon}} \\ y_i & \leftarrow \gamma \widehat{x}_i + \beta \equiv \text{BN}_{\gamma, \beta}(x_i) \end{align*}\]Fully-connected 및 Convolutional Network에서의 Batch Normalization
Nonlinearity를 \(g\)라고 정의하면 Affine Transformation은 다음과 같은 네트워크를 말한다. \(z = g(Wu + b)\) 이 변환은 Fully-connected 및 Convolutional Network에서 모두 통용되는 형식이다. 저자들은 Batch Normalization을 수행하기 위해서는 Nonlinearity 이전 단계인 \(Wu+b\)에 수행해야 한다고 주장한다. \(u\)에다가 수행할 수도 있지 않겠냐고 생각할 수도 있겠지만 저자들은 \(Wu+b\)에다가 수행하는 이유를 다음과 같이 주장한다.
- \(u\)는 이전 단계의 레이어의 Nonlinearity 결과이므로 트레이닝 과정에서 분포가 계속 변화할 것이기 때문에 정규화가 Covariate Shift를 없애주지 못할 것임
- 반면, \(Wu+b\)는 좀 더 Symmetric하고 Non-sparse한 분포를 가졌기 때문에(더 Gaussian하다고 표현) 정규화가 더욱 효과가 있을 것
Batch Normalization은 Scaling 및 Shifting을 포함하기 때문에 Bias \(b\)의 효과가 없을 것이고 결국 Affine Transformation의 Batch Normalization 적용 결과는 다음과 같을 것이다.
\[z = g(\text{BN}(Wu))\]또한 이 과정에서 학습될 파라미터 \(\gamma^{(k)}, \beta^{(k)}\)는 각 차원들에 대해서 따로 존재한다. 즉, \(k\)는 \(k\in \{1, 2, \cdots, \text{dim}(Wu) \}\)를 만족한다.
그렇다면 Convolutional Network에서는 어떻게 수행될까? 저자들은 추가적으로 Batch Normalization이 Convolutional Property를 따르기를 원했다. 따라서 같은 Feature Map의 요소들은 함께 정규화에 사용되게 된다. 즉 미니배치 사이즈가 \(m\)이고 Featrue Map의 사이즈가 \(p\times q\)라면 Effecitve 미니배치 사이즈는 \(m' = m\cdot pq\)가 된다. 즉, 정리하자면 Convolution Kernel 하나는 같은 파라미터 \(\gamma, \beta\)를 공유하게 된다.
의문점: \(\widehat{x}\)의 역할은 무엇인가?
논문을 읽어나가다보니 의문점이 생겼다. Batch Normalization은 결국 입력 \(x\)를 \(\widehat{x}\)로 정규화를 한 후에 다시 Scaling 및 Shifting을 통해서 출력 \(y\)를 생성하는 레이어라고 볼 수 있다. 그런데 저자들은 여기서 이런식으로 파이프라인을 구성하는 이유로 다음과 같이 주장했다. “We make sure that the transformation inserted in the network can represent the identity transform.” 여기서 the transformation은 Batch Normalization을 말하는 것이고 그 말인 즉, 저자들의 의도는 \(y=\text{BN}(x)\)를 단순하게 Identity 변환으로 학습시키고 싶었다는 것이다.
그러면 여기서 의문이 생긴다. \(\widehat{x}\)는 결국 내부변환일 뿐이고 실제로 Batch Normalization은 Identity 변환일 뿐인데 여기서 \(\widehat{x}\)의 역할이 무엇인가 말이다.
논문은 엄밀하지는 않지만 나름의 \(\widehat{x}\)의 역할에 대해서 서술해놓고 있다. 또한 \(\widehat{x}\)의 역할이 중요하다고 강조도 하고있다. 논문에서는 \(\widehat{x}\)가 서브 네트워크 \(y=\gamma x + \beta\)의 입력의 역할을 하고있으며 이 입력의 분포가 일정해지면서 서브 네트워크의 학습 속도가 증가하며 결과적으로 전체 네트워크의 학습 속도가 증가한다고 주장하고 있다.
즉, 정리하면 다음과 같다.
- Batch Normalization은 다음과 같은 파이프라인으로 구성됨: 이전 레이어 \(\rightarrow\) 정규화 \(\rightarrow\) Linear \(\rightarrow\) 다음 레이어
- 여기서 정규화 부분의 역할: 다음 레이어에 일정한 분포를 가진 입력을 제공
- Linear 부분의 역할: 이전 레이어의 학습이 잘 이루어지기 위한 Representation Power 제공 (Network Capacity를 유지할 수 있게한다고 표현)
저자들이 주장하는 Batch Normalization의 유용함
논문의 저자들이 주장하는 Batch Normalization의 장점들을 요약하면 다음과 같다.
- 높은 Learning Rate를 설정 가능: 결과적으로 더 빠른 트레이닝
- 트레이닝 시에 Deterministic하지 않은 결과 생성 \(\rightarrow\) Regularization 효과: 결과적으로 Dropout을 사용하지 않아도 됨
- Learning Rate Decay를 더 느리게 설정 가능
실험 1: MNIST
Activation의 분포가 일정함을 보이기 위해서 다음의 실험을 구성하였다. MNIST 데이터셋을 이용하여 손글씨 이미지를 Classification하는 모델을 Hidden Size를 100으로 가지는 3개의 Fully-connected 레이어로 구성하였다. 각각의 레이어는 Sigmoid Nonlinearity를 가진다. 각각의 Weight는 Gaussian 분포를 갖게끔 초기화를 하였으며 마지막 레이어의 사이즈는 10으로 하여 0~9의 클래스를 분류하게끔 하였다. 그 외의 자세한 트레이닝 Config는 논문에 자세히 설명되어 있다.
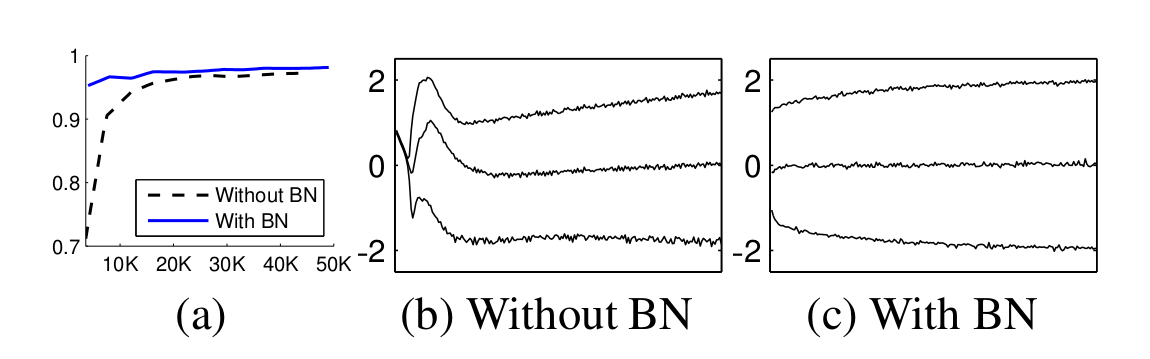
그림은 실험에 대한 결과이다. (a)에서 확인할 수 있듯이 확실히 Batch Normalization을 사용했을 경우에 더 빨리 수렴하고 Accuracy도 높다는 것을 확인할 수 있다. (b)와 (c)는 각각 Batch Normalization을 썼을 경우와 그렇지 않은 경우의 Sigmoid의 입력 분포를 트레이닝 과정동안 보여주는 그래프이다. 확실히 Batch Normalization을 사용했을 경우에 더 분포가 안정적이고 일정하다는 점을 확인할 수 있다.
실험 2: ImageNet Classification
실험 2에서는 Inception Network에 Batch Normalization을 적용하여 결과를 확인하였다. 자세한 Config는 논문에 잘 정리되어 있다. 데이터셋은 ImageNet의 LSVRC2012 트레이닝 데이터를 사용하였다고 한다. 결과는 아래 그림과 같다.
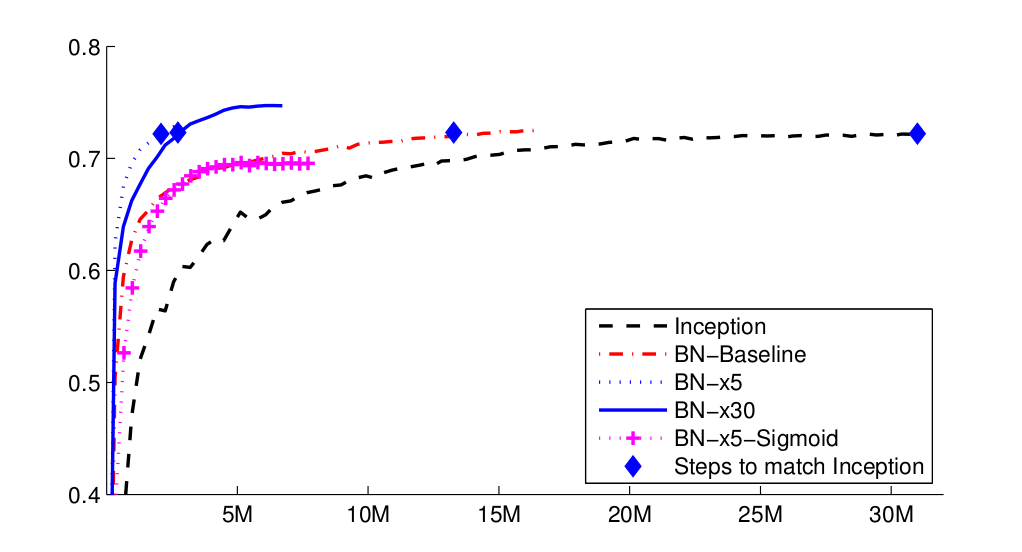
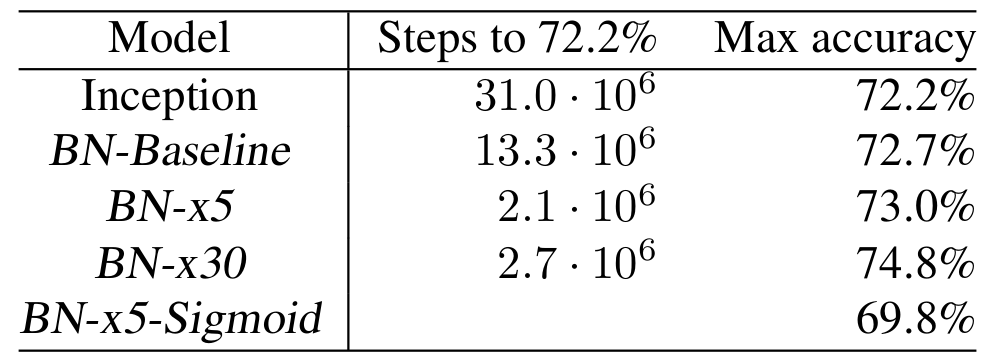
결과를 좀 더 자세히 정리하면 다음과 같다.
- Inception: Inception Network 베이스라인 모델이다. Learning Rate는 0.0015를 사용하였다.
- BN-Baseline: 위의 Inception과 동일하지만 Nonlinearity에 들어가기 전에 Batch Normalization을 적용한 모델이다.
- BN-x5: 위의 베이스라인 모델과 같지만 Learning Rate를 5배인 0.0075를 사용한 모델이다.
- BN-x30: 마찬가지로 Learning Rate를 30배로 사용한 모델이다.
- BN-x5-Sigmoid: BN-x5와 동일하지만 Nonlinearity를 ReLU 대신 Sigmoid를 사용한 모델이다.
확실히 Batch Normaliazation을 사용하면 더 큰 Learning Rate에 대해서도 더 빠른 수렴 및 성능을 보장한다고 볼 수 있을 것이다.
그 다음 결과는 앙상블 모델을 이용한 Classification 결과이다. 이번 결과에서도 Batch Normalization이 새로운 State-of-the-art 수준을 제시한다고 주장한다.
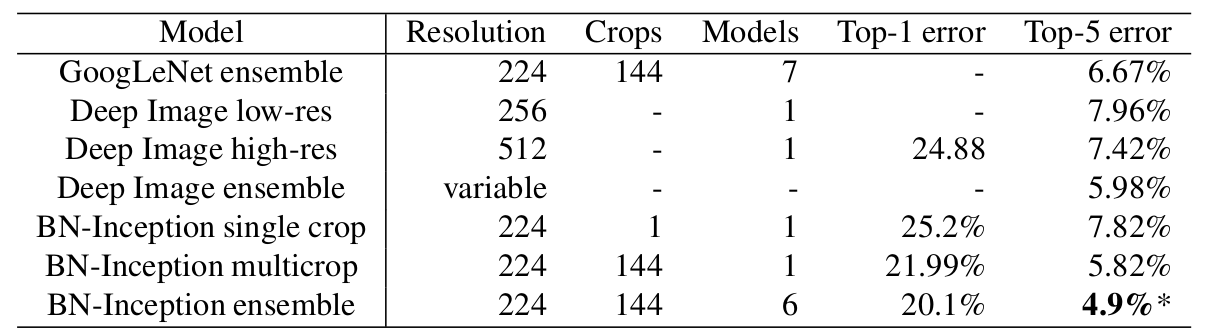
TensorFlow Module 사용법
Batch Normalization은 TensorFlow에 잘 모듈화가 되어있기 때문에 사용하는데 큰 어려움은 없다. 다만 몇가지 주의해야할 사항들이 있어서 정리를 해놓는다.
먼저 TensorFlow에서 Batch Normalization을 사용하는 예제는 아래와 같다.
import tensorflow as tf
import hyparams as hp
inputs, labels = dataset_loader.get_batch(batch_size=hp.batch_size)
convs1 = tf.layers.conv1d(
inputs=inputs,
filters=hp.filters_list[0],
kernel_size=hp.kernel_size_list[0],
padding="same")
bns1 = tf.layers.batch_normalization(inputs=convs1, training=hp.training)
convs2 = tf.layers.conv1d(
inputs=bns1,
filters=hp.filters_list[1],
kernel_size=hp.kernel_size_list[1],
padding="same")
outputs = convs2
tf.layers.batch_normalization을 사용하면 간편하게 Batch Normalization을 적용할 수 있다. 여기서 주의할 점은 training인자를 정확하게 넣어줘야 한다는 점이다. 현재가 트레이닝이 진행되는 상황이면 training=True, 그렇지 않고 단순하게 인퍼런스에 사용되는 상황이면 training=False를 해줘야 한다. 그 이유는 앞서 정리하였듯이 Batch Normalization이 트레이닝하는 경우와 인퍼런스하는 경우에 연산 과정이 조금 달라지기 때문이다.
그 다음으로 주의해야 할 사항은 다음과 같다. Batch Normalization의 연산은 다른 레이어들의 연산과는 조금 다르기 때문에 Optimizer를 설정해줄 때 조금 다르게 해주어야 한다. 먼저 기존의 방식대로 Optimizer를 정의해보자.
loss = tf.nn.softmax_cross_entropy_with_logits(labels=labels, logits=outputs)
opt = tf.train.AdamOptimizer(learning_rate=hp.learning_rate).minimize(loss)
평범하게 Adam Optimizer를 사용하여 정의하였다. 이 경우에 발생하는 문제는 보통 트레이닝 과정에서는 발견되지 않지만 인퍼런스를 하는 도중에 발생하곤 한다. 공식 홈페이지에는 다음과 같은 경고가 쓰여져 있다.
이 경고를 해석해보자면 TensorFlow 상에서 Batch Normalization에 사용되는 여러 Trainable Parameter들을 제외한 Moving Mean 및 Moving Variance는 디폴트로 tf.GraphKeys.UPDATE_OPS에 위치하며 따라서 따로 Dependency 설정을 해주지 않으면 연산이 되지 않는다는 설명이다. 즉 모델을 트레이닝하기 전에 현재 배치로부터 Moving Mean 및 Moving Variance를 미리 계산해주어야 하며 그러기 위해서는 따로 설정을 추가해줘야 한다는 의미이다.
TensorFlow 공식 홈페이지에서 설명하는대로 위의 예제를 수정하면 아래와 같다.
loss = tf.nn.softmax_cross_entropy_with_logits(labels=labels, logits=outputs)
opt = tf.train.AdamOptimizer(learning_rate=hp.learning_rate)
update_ops = tf.get_collection(tf.GraphKeys.UPDATE_OPS)
with tf.control_dependencies(update_ops):
opt = opt.minimize(loss)
마지막으로 아주 마이너한 문제지만 문제가 될 수 있는 부분을 짚고 넘어가려고 한다. 보통 트레이닝 이후에 모델을 저장하곤 하는데 tf.train.Saver를 이용하게 된다. 이 때 인자로 var_list를 넣어줄 수 있는데 만약 여기에 아래와 같이 tf.trainabe_variables()로 설정하게 된다면 Batch Normalization의 학습 결과로 생성된 Moving Mean 및 Moving Variance가 제대로 저장이 되지 않는 문제가 발생하니 주의하도록 하자.
saver = tf.train.Saver(var_list=tf.trainable_variables(), max_to_keep=1000)
저장을 하기 위한 tf.train.Saver를 활용하는 경우 위와 같은 실수를 방지하기 위해서는 그냥 아래처럼 var_list 인자는 비워두도록 하자. 그러면 디폴트로 저장가능한 모든 변수들이 저장된다.
saver = tf.train.Saver(max_to_keep=1000)
아래의 에러 메시지는 방금처럼 var_list=tf.trainable_variables()로 설정하고 불러올때는 var_list 인자를 비워두고 실행하였을 경우에 발생하는 메시지이다. 메시지에서 확인할 수 있듯이 Moving Mean이 제대로 저장되지 않아서 불러올 수 없게 되었다.
NotFoundError (see above for traceback): Restoring from checkpoint failed. This is most likely due to a Variable name or other graph key that is missing from the checkpoint. Please ensure that you have not altered the graph expected based on the checkpoint. Original error:
Key encoder/encoder_cbhg/conv_bank/batch_normalization/moving_mean not found in checkpoint
[[Node: save/RestoreV2 = RestoreV2[dtypes=[DT_FLOAT, DT_FLOAT, DT_FLOAT, DT_FLOAT, DT_FLOAT, ..., DT_FLOAT, DT_FLOAT, DT_FLOAT, DT_FLOAT, DT_FLOAT], _device="/job:localhost/replica:0/task:0/device:CPU:0"](_arg_save/Const_0_0, save/RestoreV2/tensor_names, save/RestoreV2/shape_and_slices)]]
