Optimal Classifier
일반적으로 Classification 문제는 샘플 공간 \(\mathcal{X}\) 상에 있는 샘플 \(\mathbf{x}_1, \mathbf{x}_2, \cdots \in \mathcal{X}\) 각각에 대해서 이 샘플은 어떤 클래스 \(y \in \mathcal{Y}\)로 분류할 것인가에 관한 문제로 생각할 수 있을 것이다. 이러한 문제 세팅에서 자연스럽게 우리는 Classifier \(f\)를 정의할 수 있다. Classifier \(f:\mathcal{X} \longmapsto \mathcal{Y}\)는 주어진 샘플 공간으로부터 클래스 공간으로 Mapping해주는 함수라고 정의할 수 있을 것이다. 예를 들면 다음과 같다. 여러 음식들(\(\mathcal{X}\))을 과일이냐 아니냐(\(\mathcal{Y}=\{0, 1 \}\))로 분류하는 Classifier \(f\)를 예로 들어보자. \(f\)는 다음과 같이 동작할 것이다.
\[f(\text{Apple}) = 1, \ \ \ f(\text{Banana}) = 1, \ \ \ f(\text{Steak}) = 0, \cdots\]물론 어떤 Classifier \(g\)는 다음과 같이 동작할 수도 있을 것이다.
\[g(\text{Apple}) = 1, \ \ \ g(\text{Banana}) = 0, \ \ \ g(\text{Steak}) = 0, \cdots\]이 경우 \(f\)는 바나나에 대해서는 정확히 분류해냈지만 \(g\)는 그2렇지 못한 셈이 되었다. 우리는 바나나가 과일이 맞다는 것을 알 수 있으므로 \(g\) 보다는 \(f\)가 더 성능이 좋다고 판단할 수 있다.
위와 같은 예시를 바탕으로 Optimal Classifier를 정의할 수 있다. 일단 Optimal Classifier의 정의는 다음과 같다.
\[f^*(\mathbf{x}) = \arg \max_{Y=y}P(Y=y \vert X=\mathbf{x})\]위의 과일 예시로 다시 설명을 해보자. 실제 자연계의 모델은 주어진 음식 \(\mathbf{x}\)에 대해서 과일인지 아닌지에 대한 분포 \(P(Y\vert X=\mathbf{x})\)를 모델링하고 있다고 가정할 수 있다. (물론 이 가정은 틀렸을 수도 있다.) 이러한 분포를 최대로 만족하는 Classifier \(f\)가 바로 Optimal Classifier가 될 것이다. 이러한 Optimal Classifier를 찾기 위해서는 다음과 같은 Optimization 문제를 풀어야 할 것이다.
\[f^* = \arg \max_f P(Y=f(\mathbf{x}) \vert X=\mathbf{x}), \ \forall \mathbf{x} \in \mathcal{X}\]Machine Learning의 방법론은 이러한 Optimal Classifier를 찾기 위한 모델링을 크게 2가지로 분류하고 있다. Discriminative Model과 Generative Model이다.
Discriminative Model 및 Generative Model
Discriminative Model은 \(P(Y\vert X)\)에 대한 가정을 추가하여 \(P(Y\vert X)\)를 직접 모델링을 하게 되며 이렇게 찾아낸 \(P(Y\vert X)\)를 이용하여 Decision Boundary를 찾는 것이이다. Discriminative Model의 대표적인 방법은 Linear Regression 및 Logistic Regression이 있다.
Generative Model은 Bayes Theorem을 이용하여 \(P(Y\vert X)\)를 \(P(X \vert Y)P(Y)\)로 분해하여 \(P(X\vert Y)\)와 \(P(Y)\)에 대한 가정을 추가하여 간접적으로 \(P(Y\vert X)\)를 모델링하여 Decision Boundary를 찾게 된다. Generative Model의 대표적인 방법은 Naive Bayes Classification이 있다.
일반적으로 확률 모델 \(P(X\vert Y)\)나 \(P(Y)\)에 대한 좋은 가정을 할 수 있다면 적은 데이터로도 충분히 좋은 성능을 찾아낼 수 있다는 것이 Generative Model의 장점이다. 반면 Discriminative Model은 데이터가 충분히 많다면 훨씬 더 좋은 성능을 낼 수 있다. 이러한 관점으로 봤을 때 Discriminative Model은 MLE(Maximum Likelihood Estimation)와 같다고 볼 수 있으며 Generative Model은 MAP(Maximum A Posteriori)와 같다고도 볼 수 있다.
Logistic Regression
Logistic Regression은 위에서 설명하였듯이 Discriminative Model의 한 종류이다. 따라서 \(P(Y\vert X)\)에 대해서 가정을 하여 \(P(Y\vert X;\boldsymbol{\theta})\)로 모델링을 하게 된다. 문제를 좀 더 간단하게 표현하기 위해서 클래스 공간 \(\mathcal{Y}\)는 Binary라는 가정(\(\mathcal{Y}=\{0,1\}\))을 추가하자. 물론 Multi 클래스에 대해서 간단한 방법으로 확장이 가능하다. \(P(Y\vert X)\)가 Binary 랜덤 변수에 대한 분포를 나타내므로 Bernoulli 분포로 가정을 하는 것이 자연스러울 것이다.
\[\begin{align*} P(Y=y \vert X=\mathbf{x};\boldsymbol{\theta}) & = p_{\boldsymbol{\theta}}(\mathbf{x})^y(1−p_{\boldsymbol{\theta}}(\mathbf{x}))^{1−y} \\ p_{\boldsymbol{\theta}}(\mathbf{x}) & = P(Y=1\vert X=\mathbf{x};\boldsymbol{\theta}) \end{align*}\]여기서 \(p_{\boldsymbol{\theta}}(\mathbf{x})\)를 Logistic Function으로 가정하는 것이 Logistic Regression이다. 대표적인 Logistic Function들은 다음과 같다.
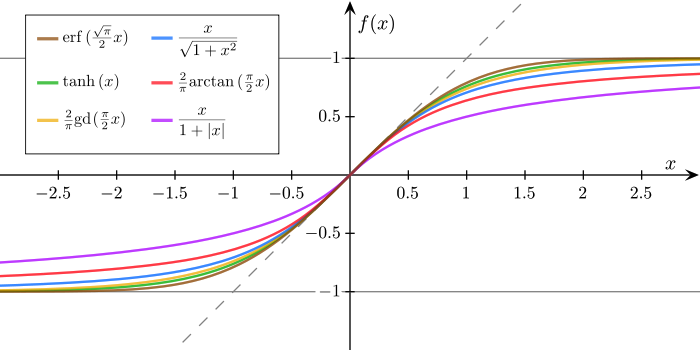
(출처: https://aailab.kaist.ac.kr/xe2/page_GBex27)
여기서는 가장 대표적인 Logistic Function인 Sigmoid를 사용하기로 하자. Sigmoid를 사용하여 \(p_{\boldsymbol{\theta}}(\mathbf{x})\)를 다음과 같이 정의할 수 있다.
\[\begin{align*} p_{\boldsymbol{\theta}}(\mathbf{x}) & = \sigma(\boldsymbol{\theta}^{\text{T}}\mathbf{x}) \\ & = \frac{1}{1+e^{−\boldsymbol{\theta}^{\text{T}}\mathbf{x}}} \end{align*}\]이렇게 모델링이 된 \(P(Y\vert X;\boldsymbol{\theta})\)를 주어진 데이터셋 \(D\)를 이용하여 Fitting시키는 문제를 Logistic Regression이라고 한다.
Logistic Regression을 풀기 위해서는 Optimal Classifier를 찾는 Optimization 문제로부터 시작하는 것이 좋다.
\[\begin{align*} f^*(\mathbf{x}) & = \arg \max_{Y=y} P(Y=y \vert X=\mathbf{x}) \end{align*}\]여기서 우리는 실제 \(P(Y=y \vert X=\mathbf{x})\)를 알 수 없으므로 우리가 가정한 모델 \(P(Y=y \vert X=\mathbf{x} ; \boldsymbol{\theta})\)를 대신 사용하여 Optimal Classifier를 정의하게 된다.
\[\begin{align*} f^*(\mathbf{x}) & = \arg \max_{Y=y} P(Y=y \vert X=\mathbf{x} ; \boldsymbol{\theta}) \end{align*}\]우리는 이제 이 Optimization 문제로부터 실제 \(P(Y=y\vert X=\mathbf{x})\)를 모델링할 수 있는 최적의 파라미터 \(\boldsymbol{\theta}\)를 찾고자 한다. 이 경우 우리에게 주어진 데이터셋 \(D\)를 활용하게 된다. 즉, 데이터셋 \(D\)를 가장 잘 설명할 수 있는 파라미터 \(\boldsymbol{\theta}\)를 찾는 MLE 방법을 사용하게 된다. 여기서는 데이터셋 \(D\) 내부의 \(\mathbf{x}\)와 \(y\)가 서로 Dependent하기 때문에 MCLE(Maximum Conditional Likelihood Estimation)를 사용하게 된다. Binary 세팅에서 MCLE를 풀기 위한 Optimization 문제는 Binary Cross-Entropy Loss를 최소화하는 문제와 동치라는 것을 다음의 포스팅에서 확인할 수 있다. 여기서는 받아들이고 사용하도록 하자.
\[\begin{align*} \boldsymbol{\theta}^* & = \arg \max_{\boldsymbol{\theta}} P(D ; \boldsymbol{\theta}) \\ & = \arg \min_{\boldsymbol{\theta}} \sum_{(\mathbf{x}, y) \in D} -\left[ y\log (p_{\boldsymbol{\theta}}(\mathbf{x})) + (1-y)\log(1-p_{\boldsymbol{\theta}}(\mathbf{x})) \right] \end{align*}\]이러한 Optimization 문제는 Closed Form으로 풀어내기 쉽지 않으며 따라서 Iterative한 방법으로 접근을 하게 된다. 가장 대표적인 Iterative한 방법은 바로 Gradient Descent(Ascent)이다. Gradient Descent에 대한 기본적인 내용 정리는 다음의 포스팅에서 확인할 수 있다.
Naive Bayes
Naive Bayes 방법은 위에서 설명한대로 Generative Model의 한 종류이다. 따라서 \(P(Y\vert X)\)를 직접 가정하여 모델링하는 대신 \(P(X\vert Y)\) 및 \(P(Y)\)에 대한 가정이 필요하게 된다. 위에서 Logistic Regression을 설명할 때 사용한 문제 세팅을 그대로 가져와서 Optimization 문제를 다시 써보면 다음과 같이 쓸 수 있다.
\[\begin{align*} f^*(\mathbf{x}) & = \arg \max_{Y=y} P(Y=y \vert X=\mathbf{x}) \end{align*}\]Generative Model은 위에서 설명한대로 아래와 같이 Optimization 문제를 분해하여 생각하게 된다.
\[\begin{align*} f^*(\mathbf{x}) & = \arg \max_{Y=y} P(X=\mathbf{x} \vert Y=y)P(Y=y) \end{align*}\]여기서 Generative Model은 다양한 방법으로 \(P(X=\mathbf{x} \vert Y=y)\)을 모델링하게 되는데 여기서는 한 가지 문제가 발생하게 된다. 바로 이 확률을 추정하기 위해서 필요한 데이터셋의 크기이다. 만약 \(\mathbf{x}\)의 Dimension이 \(d\)이고, 각각의 Dimension의 Element는 Binary라고 가정하였을 경우 \(P(X=\mathbf{x} \vert Y=y)\)를 추정하기 위해서 필요한 \((\mathbf{x}, y)\) Tuple의 갯수는 \((2^d-1)k\)가 될 것이다. 이 크기는 너무 크다는 문제가 있으며 이것을 줄이기 위한 다른 추가적인 가정을 필요로 하게 된다.
따라서 Naive Bayes는 한 가지 가정을 추가하여 이 문제를 해결하려고 시도하게 된다. 바로 Conditional Independence 가정이다. Conditional Independence는 다음과 같이 정의된다. 확률 변수 \(X_1, X_2, Y\)에 대해서 각각이 다음을 만족할 때 \(X_1\)은 Given \(Y\)에 대해서 \(X_2\)와 Conditional Independent하다고 정의한다.
\[P(X_1 \vert X_2, Y) = P(X_1 \vert Y)\]따라서 이러한 Conditional Independence 가정을 통해서 Naive Bayes의 Optimization 문제는 아래와 같이 쓸 수 있다.
\[\begin{align*} f^*(\mathbf{x}) & = \arg \max_{Y=y} P(X=\mathbf{x} \vert Y=y)P(Y=y) \\ & = \arg \max_{Y=y} P(Y=y) \prod_{i\in \{1,2,\cdots, d\}} P(X^{(i)}=x^{(i)} \vert Y=y) \\ & \text{where} \ X=(X^{(1)}, X^{(2)}, \cdots, X^{(d)}), \ \mathbf{x} = (x^{(1)}, x^{(2)}, \cdots, x^{(d)}) \end{align*}\]이 경우 확률을 추정하기 위한 데이터셋의 크기가 매우 감소하는 것을 확인할 수 있다. \(P(X^{(i)}=x^{(i)} \vert Y=y)\)를 추정하기 위해 필요한 \((x^{(i)}, y)\) Tuple는 \(k\)개가 될 것이고 \(x^{(i)}\)가 \(d\)개가 필요할 것이기 때문에 총 Tuple의 갯수는 \(dk\)가 될 것이다.
Conditional Independence 가정이 합당한지에 대해서는 Graphical Model에 대한 공부가 더 필요하다. 나중에 공부하여 정리하도록 하겠다.
어쨌든 Naive Bayes 방법을 정리하면, 일반적인 Generative Model처럼 \(P(X\vert Y)\)에 대해서 가정을 통하여 모델링을 시도하게 되지만 여기서 사용하는 가정이 Conditional Independence 가정이 사용된다면 그 방법은 Naive Bayes 방법을 사용한다고 말할 수 있겠다.
Logistic Regression과 Naive Bayes의 관계
두 방법을 비교하기 위해서 Naive Bayes의 가정이 몇 가지 더 추가되게 된다. 일단 기본적으로 \(P(X\vert Y)\)가 기본적으로 \(X\)의 모든 Dimension Element에 대해서 Conditional Independence라는 가정에 추가하여 특정 파라미터 \(\boldsymbol{\theta}\)로 Parameterization하였다고 가정한다. 대부분의 강의자료 또는 교과서에서는 \(P(X\vert Y)\)를 Gaussian이라고 가정하는데 여기서는 좀 더 일반적으로 가정하도록 해보자. \(P(X\vert Y)\)를 다음과 같이 가정하자.
\[P(X=\mathbf{x} \vert Y=y ; \boldsymbol{\theta}) = q_{(y, \boldsymbol{\theta})}(\mathbf{x})\]또한 Naive Bayes는 Conditional Independence 가정을 사용하기 때문에 아래와 같은 가정이 추가된다.
\[\begin{align*} P(X=\mathbf{x} \vert Y=y ; \boldsymbol{\theta}) & = q_{(y, \boldsymbol{\theta})}(\mathbf{x}) \\ & = \prod_{i\in \{1,2,\cdots, d \}} q_{(y, \boldsymbol{\theta})}^{(i)}(x^{(i)}) \end{align*}\]마찬가지로 \(P(Y)\)에 대해서도 가정이 필요하다. 다음과 같은 가정을 사용하도록 하자.
\[P(Y=y) = \pi_y\]이제 모든 가정이 끝났다. 이제 우리가 찾고자 하는 \(P(Y\vert X)\)를 파라미터 \(\boldsymbol{\theta}\)에 대해서 모델링해보도록 하자. 먼저 \(P(Y\vert X)\)를 다음과 같이 써보자.
\[\begin{align*} P(Y=y\vert X=\mathbf{x}) & = \frac{P(X=\mathbf{x} \vert Y=y)P(Y=y)}{P(X=\mathbf{x})} \end{align*}\]여기서 Naive Bayes의 가정을 통해서 \(P(X=\mathbf{x}\vert Y=y)\)를 \(P(X=\mathbf{x}\vert Y=y ; \boldsymbol{\theta})\)로 다시 써보도록 하자.
\[\begin{align*} P(Y=y\vert X=\mathbf{x} ; \boldsymbol{\theta}) & = \frac{P(X=\mathbf{x} \vert Y=y ; \boldsymbol{\theta})P(Y=y)}{P(X=\mathbf{x})} \\ & = \frac{P(X=\mathbf{x} \vert Y=y ; \boldsymbol{\theta})P(Y=y)}{\sum_{y\in \{ 0,1 \}}P(X=\mathbf{x} \vert Y=y ; \boldsymbol{\theta})P(Y=y)} \\ & = \frac{\prod_{i\in \{1,2,\cdots, d \}} q_{(y, \boldsymbol{\theta})}^{(i)}(x^{(i)})\pi_y}{\sum_{y\in \{ 0,1 \}}\prod_{i\in \{1,2,\cdots, d \}} q_{(y, \boldsymbol{\theta})}^{(i)}(x^{(i)})\pi_y} \\ & = \frac{\prod_{i\in \{1,2,\cdots, d \}} q_{(y, \boldsymbol{\theta})}^{(i)}(x^{(i)})\pi_y}{\prod_{i\in \{1,2,\cdots, d \}} q_{(0, \boldsymbol{\theta})}^{(i)}(x^{(i)})\pi_0 + \prod_{i\in \{1,2,\cdots, d \}} q_{(1, \boldsymbol{\theta})}^{(i)}(x^{(i)})\pi_1} \end{align*}\]Logistic Regression과의 관계를 확인하기 위해서는 Logistic Regression의 \(p_{\boldsymbol{\theta}}(\mathbf{x})\)에 대한 가정이 Naive Bayes에서는 어떤 모습으로 변화하였는지를 확인해야 할 것이다. Logistic Regression에서 \(p_{\boldsymbol{\theta}}(\mathbf{x})\)는 \(P(Y=1\vert X=\mathbf{x} ; \boldsymbol{\theta})\)를 의미하므로 위에서 구한 \(P(Y=y\vert X=\mathbf{x} ; \boldsymbol{\theta})\)를 이용하여 \(p_{\boldsymbol{\theta}}(\mathbf{x})\)를 써보도록 하자.
\[\begin{align*} p_{\boldsymbol{\theta}}(\mathbf{x}) & = \ P(Y=1\vert X=\mathbf{x} ; \boldsymbol{\theta}) \\ & = \ \frac{\prod_{i\in \{1,2,\cdots, d \}} q_{(1, \boldsymbol{\theta})}^{(i)}(x^{(i)})\pi_1}{\prod_{i\in \{1,2,\cdots, d \}} q_{(0, \boldsymbol{\theta})}^{(i)}(x^{(i)})\pi_0 + \prod_{i\in \{1,2,\cdots, d \}} q_{(1, \boldsymbol{\theta})}^{(i)}(x^{(i)})\pi_1} \\ & = \ \frac{1}{1 + \frac{\prod_{i\in \{1,2,\cdots, d \}} q_{(0, \boldsymbol{\theta})}^{(i)}(x^{(i)})\pi_0}{\prod_{i\in \{1,2,\cdots, d \}} q_{(1, \boldsymbol{\theta})}^{(i)}(x^{(i)})\pi_1}} \\ & = \ \frac{1}{1 + \exp \left( -\log \left[ \frac{\prod_{i\in \{1,2,\cdots, d \}} q_{(1, \boldsymbol{\theta})}^{(i)}(x^{(i)})\pi_1}{\prod_{i\in \{1,2,\cdots, d \}} q_{(0, \boldsymbol{\theta})}^{(i)}(x^{(i)})\pi_0} \right] \right) } \\ & = \ \frac{1}{1 + \exp \left( -\left[ \sum_{i\in \{1,2,\cdots, d \}} \log q_{(1, \boldsymbol{\theta})}^{(i)}(x^{(i)}) - \sum_{i\in \{1,2,\cdots, d \}} \log q_{(0, \boldsymbol{\theta})}^{(i)}(x^{(i)}) + \log \pi_1 - \log \pi_0 \right] \right) } \\ & = \ \sigma \left( \sum_{i\in \{1,2,\cdots, d \}} \log q_{(1, \boldsymbol{\theta})}^{(i)}(x^{(i)}) - \sum_{i\in \{1,2,\cdots, d \}} \log q_{(0, \boldsymbol{\theta})}^{(i)}(x^{(i)}) + \log \pi_1 - \log \pi_0 \right) \end{align*}\]결과를 살펴보면 Logistic Regression의 가정과는 다르게 Naive Bayes는 좀 더 복잡한 가정들이 포함된 모델이라는 점을 확인할 수 있다. 데이터의 특성이 이러한 가정을 잘 따르는 경우라면 위에서 언급했듯이 더 적은 데이터로도 좋은 모델 파라미터를 잘 찾아낼 수 있을 것이라고 정리할 수 있을 것이다. 하지만 데이터가 많이 있는 경우라면 충분히 Logistic Regression의 간단한 구조의 모델로 충분히 데이터의 특성을 잘 반영하는 파라미터를 찾아낼 수 있을 것이다.