지난번에 Bahdanau Attention에 대한 포스팅을 작성하였으며 그 후속으로 이번에는 Luong Attention에 대한 내용을 정리하게 되었다. Bahdanau Attention에 대한 포스팅은 다음의 링크를 통해서 확인할 수 있다.
또한 이번 포스팅은 다음의 논문을 스터디하여 정리하였다:
Notation
이전 포스팅에 이어서 이번 포스팅에서도 다음의 Notation을 사용할 것이다.
- \(\mathcal{X} = (\mathbf{x}_t)_{t=1}^{T_{\mathbf{x}}} \in \mathbb{R}^{n \times T_{\mathbf{x}}}\): 소스 문장의 단어 One-Hot 인코딩 시퀀스
- \(\mathcal{Y} = (\mathbf{y}_t)_{t=1}^{T_{\mathbf{y}}} \in \mathbb{R}^{m \times T_{\mathbf{y}}}\): 타겟 문장의 단어 One-Hot 인코딩 시퀀스
- \(T_{\mathbf{x}}, T_{\mathbf{y}}\): 각각 \(\mathcal{X}, \mathcal{Y}\)의 시퀀스 길이 (문장의 길이)
- \(\mathbf{x}_t, \mathbf{y}_t\): 각각 \(t\)번째 타임 스텝 단어의 One-Hot 인코딩
- \(\widehat{\mathcal{Y}} = (\widehat{\mathbf{y}}_t)_{t=1}^{T_{\mathbf{y}}}\): 모델이 타겟 문장의 단어 One-Hot 인코딩 시퀀스를 추정하기 위해서 사용하는 확률 모델 \(\widehat{\mathbf{y}}_t\)의 시퀀스
Bahdanau Attention으로부터 달라진 점
논문에서 제시하는 Bahdanau Attention과의 차이점은 다음과 같이 정리할 수 있다.
- 디코더의 Hidden State Vector를 구하는 방식이 간소화되었고 결과적으로 Attention Mechanism의 Computation Path가 간소화되었다.
- Local Attention과 그것을 위한 Alignment Model을 제시하였다.
- 다양한 Score Function들을 제시하였고 그들 각각을 비교해 보았다.
사실 이 논문에서 주된 내용은 Hidden State Vector를 구하는 방식이 달라졌다는 점과 Local Attention을 사용했다는 점 말고는 특이한 점은 없다. 특히 다양한 Score Function을 제시하였다는 내용은 너무도 마이너해보인다. 아마 비슷한 시기에 비슷한 내용으로 논문을 준비하다보니 벌어진 현상으로 보인다. 어쨌든 Hidden State Vector를 어떻게 구했는지, 그리고 Local Attention이 무엇인지를 중점적으로 보면 될 듯 싶다.
Hidden State Vector
Luong Attention이 Bahdanau Attention과 가장 많이 달라진 점은 바로 Hidden State Vector를 구하는 방식이 될 것이다. 먼저 Bahdanau Attention에서는 어떤 방식으로 Hidden State Vector를 구하는지 그림으로 확인해보자. 아래의 그림은 Bahdanau Attention에서의 Computation Path를 나타낸 것이다.
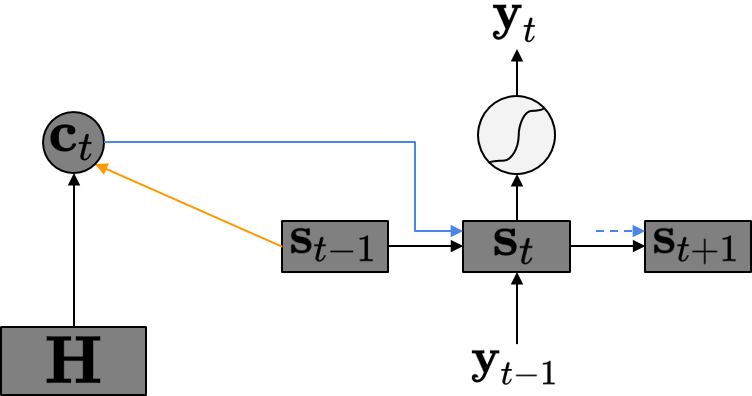
그림에서 확인할 수 있듯이 Bahdanau Attention에서는 현재 타임 스텝의 디코더 Hidden State Vector \(\mathbf{s}_t\)를 구하기 위해서 현재 타임 스텝의 Context Vector \(\mathbf{c}_t\) 및 이전 타임 스텝의 Hidden State Vector \(\mathbf{s}_{t-1}\), 그리고 현재 타임 스텝의 입력으로 들어온 \(\mathbf{y}_{t-1}\)이 사용되게 된다. 이 때 \(\mathbf{c}_t\)는 \(\mathbf{s}_{t-1}\)과 인코더 Hidden State Matrix \(\mathbf{H}\)를 이용한 Attention 메커니즘의 결과가 된다. Bahdanau Attention에서의 Attention Mechanism을 다시 정리하면 아래와 같다.
\[\begin{align*} \mathbf{c}_t & = \sum_{j=1}^{T_{\mathbf{x}}} \mathbf{a}_{tj}\mathbf{h}_j \\ & = \mathbf{H} \mathbf{a}_t \\ \mathbf{a}_t & = \text{Softmax}\left(\left(\text{Score}(\mathbf{s}_{t-1}, \mathbf{h}_j)\right)_{j=1}^{T_{\mathbf{x}}}\right) \in \mathbb{R}^{T_{\mathbf{x}}} \\ \text{Score}(\mathbf{s}_{t-1}, \mathbf{h}_j) & = \mathbf{v}^\text{T}\tanh (\mathbf{W_a}\mathbf{s}_{t-1} + \mathbf{U_a}\mathbf{h}_j) \end{align*}\]반면 Luong Attention은 \(\mathbf{s}_{t-1}\)이 아닌 \(\mathbf{s}_t\)를 이용하여 \(\mathbf{c}_t\)를 구한다. 먼저 그림을 살펴보자.
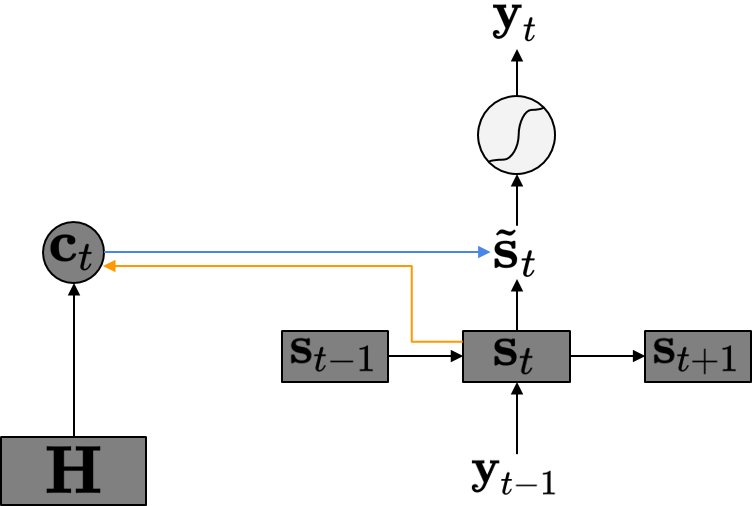
이 경우에는 Bahdanau Attention의 경우와는 다르게 \(\mathbf{c}_t\)를 구할 때 \(\mathbf{s}_{t-1}\)이 사용되는 것이 아니라 \(\mathbf{s}_t\)를 사용하게 된다. 즉, Hidden State Vector \(\mathbf{s}_t\)는 그냥 RNN의 Hidden State의 역할만을 하게 되며 출력 \(\widehat{\mathbf{y}}_t\)를 구할때는 새로운 \(\tilde{\mathbf{s}}_t\)를 거치게 된다.
이렇게 구성하게 되었을 경우에 얻을 수 있는 장점은 Computation Path가 간소화가 된다는 점을 들 수 있다. Bahdanau Attention에서는 디코더의 Hidden State의 역할을 하게되는 \(\mathbf{s}_t\)를 구할때 \(\mathbf{c}_t\)가 사용되게 되며 따라서 RNN의 재귀 연산이 수행되는 도중에 \(\mathbf{c}_t\)가 구해질 때까지 기다려야 한다. 하지만 Luong Attention의 경우에는 출력 \(\widehat{\mathbf{y}}_t\)을 구하는 부분과 RNN의 재귀 연산이 수행되는 부분을 분리할 수가 있기 때문에 더욱 Computation Path가 간소화된다고 볼 수 있다.
Luong Attention의 연산을 정리하면 다음과 같다.
\[\begin{align*} \mathbf{c}_t & = \sum_{j=1}^{T_{\mathbf{x}}} \mathbf{a}_{tj}\mathbf{h}_j \\ & = \mathbf{H} \mathbf{a}_t \\ \mathbf{a}_t & = \text{Softmax}\left(\left(\text{Score}(\mathbf{s}_{t}, \mathbf{h}_j)\right)_{j=1}^{T_{\mathbf{x}}}\right) \in \mathbb{R}^{T_{\mathbf{x}}} \end{align*}\] \[\begin{align*} \widehat{\mathbf{y}}_t & = \text{Softmax}\left( \mathbf{W_y}\tilde{\mathbf{s}}_t + \mathbf{b_y} \right) \\ \tilde{\mathbf{s}}_t & = \tanh(\mathbf{W_{ss}}\mathbf{s}_t + \mathbf{W_{cs}}\mathbf{c}_t + \mathbf{b_s}) \end{align*}\]Local Attention과 그것을 위한 Alignment Model
Luong Attention에서는 기존의 Attention Model과는 조금 다르게 Local Attention이라는 개념을 제시하였다. 먼저 기존의 Bahdanau Attention의 경우처럼 Alignment Vector가 \(\mathbf{h}_1\)부터 \(\mathbf{h}_{T_{\mathbf{x}}}\)까지의 \(T_{\mathbf{x}}\)개의 모든 벡터들을 바라보며 Attention Score를 구하게 된다. Luong Attention의 저자들은 이러한 방식을 Global Attention이라고 정의하였고 자신들은 새로운 Local Attention 방식을 제시함으로써 차별화를 시도하였다.
그러면 Local Attention은 무엇일까? 바로 \(T_{\mathbf{x}}\)개 전부를 보는 것이 아니라 특정 하이퍼파라미터 \(D\)에 대하여 \(2D+1\)개 만큼의 서브셋만을 보겠다는 것이다. 일단 Local Attention의 방법을 정리하면 아래의 식으로 정리할 수 있다.
\[\mathbf{a}_t = \text{Softmax}\left(\left(\text{Score}(\mathbf{s}_{t}, \mathbf{h}_j) \exp\left( -\frac{(j-p_t)^2}{2\sigma^2} \right) \right)_{j=p_t-D}^{p_t+D}\right) \in \mathbb{R}^{2D+1}\] \[\begin{align*} \text{where} \ \sigma = \frac{D}{2} \end{align*}\]이 때 \(p_t\)는 Aligned Position이라고 정의한다. \(p_t\)를 구하는 방식에 따라서 또 Local Attention의 방법이 달라지게 된다.
- Monotonic Alignment (local-m): \(p_t = t\)
- Predictive Alignment (local-p): \(p_t = T_{\mathbf{x}} \cdot \text{Sigmoid}\left(\mathbf{v}_p^\text{T} \tanh(\mathbf{W}_p \mathbf{s}_t)\right)\)
이렇게 구해진 \(\mathbf{a}_t\)와 범위 \([p_t-D, p_t+D]\)에 대해서 Weighted Sum을 통해서 Context Vector \(\mathbf{c}_t\)를 구한다.
\[\mathbf{c}_t = \mathbf{H}[:, p_t-D:p_t+D+1]\mathbf{a}_t\]다양한 Score Function 제시 및 비교
Luong Attention에서는 기존 Bahdanau Attention에서 제시했던 Score Function 뿐 아니라 다른 Score Function들에 대해서도 분석을 했다. 저자들은 4가지의 Score Function을 제시하였는데 크게 Content-Based Function과 Location-Based Function으로 나누었다. 참고로 사실상 Location-Based Function은 Attention이 필요함을 보이기 위해서 억지로 만든 개념이라고 봐도 될 것 같다. 실제로 Attention이 전혀 개입되지 않는 Score Function이기 때문이다.
- Content-Based Function:
- Location-Based Function:
Input Feeding Approach
Luong Attention의 저자들이 가졌던 또 다른 불만은 다음과 같다. 왜 현재 타임 스텝의 Alignment를 구할때 이전 타임 스텝들의 Alignment들을 사용하지 않는 것일까? 저자들은 이 불만을 해소하기 위해서 Input Feeding이라는 구조를 제시하였다.
사실 말은 그럴듯하지만 별것은 아니다. 현재 타임 스텝의 입력 \(\mathbf{y}_{t-1}\)이 들어갈 때 이전 타임 스텝의 새로운 Hidden State Vector \(\tilde{\mathbf{s}}_{t-1}\)을 함께 Concatenate하여 넣어주는 것이다. 아래의 그림은 Input Feeding이 이루어지는 방식을 정리한 것이다.
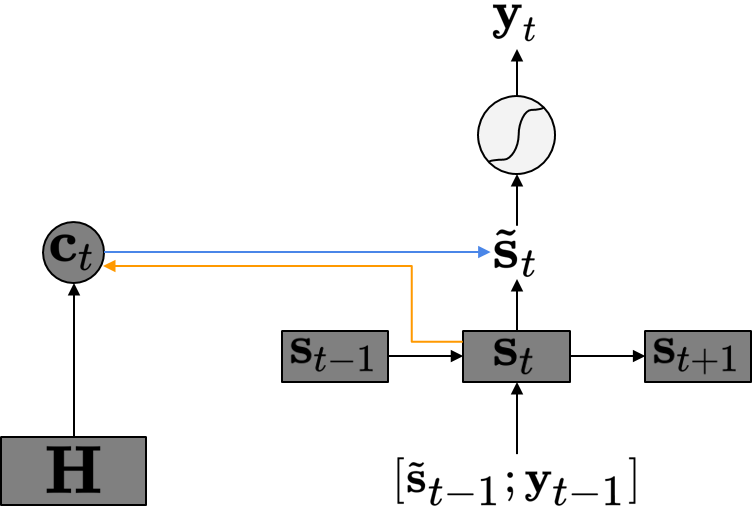
이렇게 함으로써 얻을 수 있는 장점을 저자들은 다음과 같이 정리하였다.
- 이전의 Alignment 정보들을 Fully 활용할 수 있다.
- 네트워크를 수직적/수평적으로 넓게 구현하게 되었다.
두 번째 장점은 솔직히 잘 모르겠다. 첫 번째 장점은 \(\tilde{\mathbf{s}}_{t-1}\)이 \(\mathbf{c}_{t-1}\)을 포함하고 있기 때문에 가능한 설명이다.
실험 및 성능 검증
여러 실험을 통해서 자신들의 Attention 메커니즘의 성능을 보였지만 여기서는 두 가지의 실험만을 소개하도록 하겠다.
실험은 전부 WMT’ 14 데이터셋을 이용하였다. 영어와 독일어로 구성된 Parallel 코퍼스이며 번역을 위한 데이터셋이다. 약 4.5M개의 문장 쌍이 존재하며 코퍼스에 존재하는 단어는 영어 단어 116M, 독일어 단어 110M이다. 또한 단어 사전은 자주 등장하는 순서로 50K로 제한하였으며 새로운 단어거나 사전에 없는 단어는 <Unknown> 토큰을 사용하였다. 모델은 간단한 LSTM 스택을 쌓아서 구성하였다.
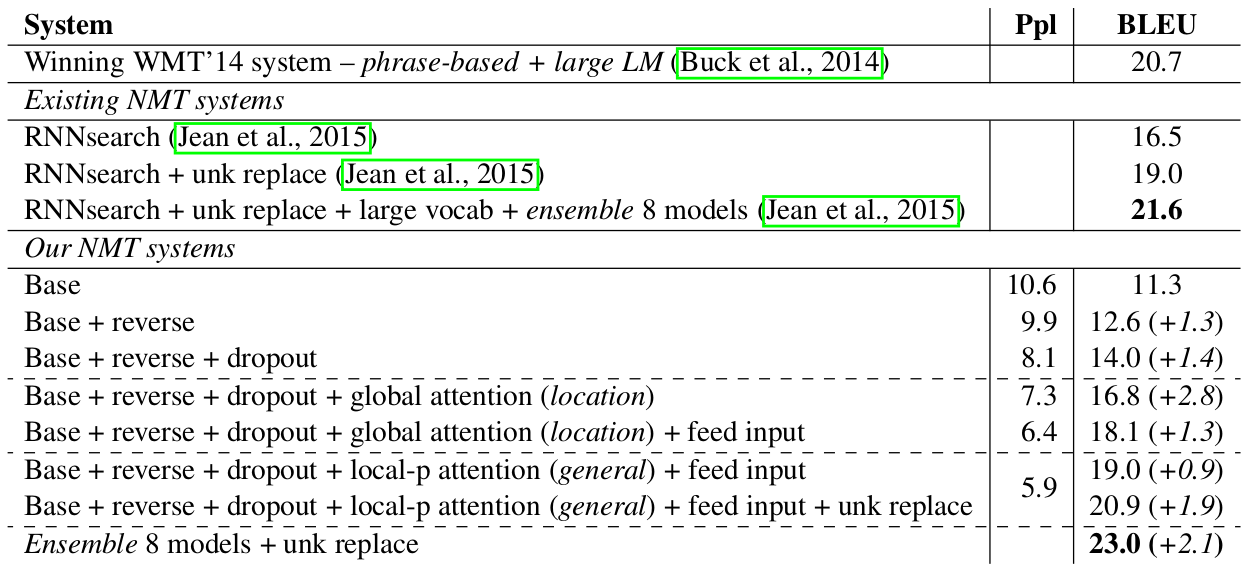
위의 테이블은 첫 번째 실험 결과이다. 자신들의 모델이 이전에 최고 성능을 보인 모델 및 Bahdanau Attention을 사용한 모델보다 낫다는 것을 보인다. 실제로 BLEU 스코어가 이전 결과들에 비해서 (8개의 앙상블 모델을 이용하였지만) 더 좋은 것을 확인할 수 있다.
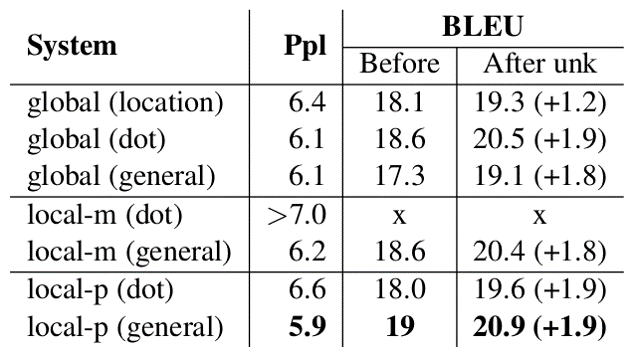
그 다음 결과는 다양한 Score Function을 이용하여 비교 및 분석을 수행한 것이다. 확실히 Global Attention 보다는 Local Attention이, Local-m 보다는 Local-p가 좋은 성능을 보인다.
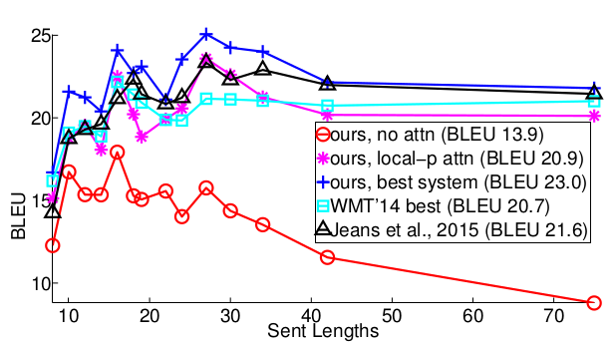
그 다음 결과는 문장의 길이가 길어질수록 성능 변화가 어떻게 되는지 보여주는 그래프이다. 문장이 길어지면 Attention을 사용하지 않는 모델은 점차 성능이 하락하는 것을 확인할 수 있으며 또한 Attention을 사용하는 모델도 이전의 모델보다는 자신들의 모델이 성능이 더 좋음을 보여준다.