이번 포스팅은 다음의 논문을 스터디하여 정리하였다:
또한 다음의 링크도 참고하여 작성하였다.
Neural Machine Translation
기계 번역은 이전부터 확률적인 접근 방법을 통해서 수행이 되어왔다. 간단히 설명하면 소스 문장 \(\mathcal{X}\)을 Conditioning하여 조건부 확률 \(p(\mathcal{Y} \vert \mathcal{X})\)를 최대화하는 타겟 문장 \(\mathcal{Y}\)를 찾는 것이다. 수식으로 정리하면 아래와 같다. \(\widehat{\mathcal{Y}}\)는 모델의 타겟 문장 \(\mathcal{Y}\)에 대한 추정 문장이다.
\[\widehat{\mathcal{Y}} = \arg \max_{\mathcal{Y}} p(\mathcal{Y} \vert \mathcal{X})\]최근 딥러닝을 이용한 연구가 활발히 진행되면서 뉴럴 네트워크를 통한 언어 번역을 시도해 보려는 NMT(Neural Machine Translation)에 관한 연구가 각광을 받게 되었다. NMT는 딥러닝 모델 \(f_{\theta}(\mathcal{X})\)를 학습시키기 위해서 Loss \(\mathcal{L}\)을 다음과 같이 사용하게 된다.
\[\mathcal{L} = -p(f_{\boldsymbol{\theta}}(\mathcal{X}) \vert \mathcal{X})\]즉, 이 Loss를 이용하여 모델 파라미터 \(\boldsymbol{\theta}\)를 다음과 같은 최적화를 통해서 학습을 시키면 된다.
\[\widehat{\boldsymbol{\theta}} = \arg \max_{\boldsymbol{\theta}} p(f_{\boldsymbol{\theta}}(\mathcal{X}) \vert \mathcal{X})\]기존의 NMT 연구는 RNN Encoder-Decoder를 이용하는 방식으로 많이 수행이 되었는데 이번에 소개하려는 논문에서는 이러한 RNN Encoder-Decoder 모델을 Attention Mechanism을 통해서 많은 개선을 이루어냈다.
논문에서 주장하는 개선 사항은 다음과 같다. 기존 RNN Encoder-Decoder는 소스 문장을 고정된 길이의 벡터로 인코딩을 하였지만 제안된 모델에서는 인코딩을 벡터들의 Sequence로 인코딩을 하여서 소스 문장의 정보가 Sequence에 쫙 펼쳐지게 되며 이것을 디코더가 스스로 어떤 벡터에 중점을 둬서 정보를 취할지 선택할 수 있게 하였다. 이 과정이 Attention Mechanism이며 이것을 처음 제안한 논문이 바로 이 논문이다.
Notation
이번 포스팅에서는 다음의 Notation을 사용할 것이다.
- \(\mathcal{X} = (\mathbf{x}_t)_{t=1}^{T_{\mathbf{x}}} \in \mathbb{R}^{n \times T_{\mathbf{x}}}\): 소스 문장의 단어 One-Hot 인코딩 시퀀스
- \(\mathcal{Y} = (\mathbf{y}_t)_{t=1}^{T_{\mathbf{y}}} \in \mathbb{R}^{m \times T_{\mathbf{y}}}\): 타겟 문장의 단어 One-Hot 인코딩 시퀀스
- \(T_{\mathbf{x}}, T_{\mathbf{y}}\): 각각 \(\mathcal{X}, \mathcal{Y}\)의 시퀀스 길이 (문장의 길이)
- \(\mathbf{x}_t, \mathbf{y}_t\): 각각 \(t\)번째 타임 스텝 단어의 One-Hot 인코딩
- \(\widehat{\mathcal{Y}} = (\widehat{\mathbf{y}}_t)_{t=1}^{T_{\mathbf{y}}}\): 모델이 타겟 문장의 단어 One-Hot 인코딩 시퀀스를 추정하기 위해서 사용하는 확률 모델 \(\widehat{\mathbf{y}}_t\)의 시퀀스
RNN Encoder-Decoder
NMT의 가장 기본적인 접근은 RNN Encoder-Decoder 모델을 이용하는 것이다. RNN Encoder-Decoder 모델은 RNN 셀을 이용하여 인코더 및 디코더를 구성하고 인코더는 번역을 하고자 하는 소스 문장을 특정 임베딩 벡터로 인코딩을 하고 디코더는 임베딩된 벡터를 타겟 언어로 번역을 하여 타겟 문장을 생성해 내는 역할을 수행하게 된다.
Encoder-Decoder 모델은 기본적으로 다음의 역할을 수행하게 된다. 모델이 현재 타임 스텝의 디코더 아웃풋 단어 One-Hot 인코딩 \(\mathbf{y}_t\)를 추정하기 위해서 인코더에 입력되는 소스 문장 \(\mathcal{X}\)와 이전 타임 스텝 디코더 아웃풋 단어 One-Hot 인코딩들인 \(\{\mathbf{y}_0, \cdots, \mathbf{y}_{t-1}\}\)이 Conditioning이 된 조건부 확률 모델 \(\widehat{\mathbf{y}} = p(\mathbf{y}_t \vert \mathbf{y}_0,\cdots, \mathbf{y}_{t-1}, \mathbf{x})\)를 모델링해야 하며 이것은 아래와 같이 기본 RNN 연산을 이용하여 모델링될 수 있다.
\[\begin{align*} \widehat{\mathbf{y}}_t & = p(\mathbf{y}_t \vert \mathbf{y}_0,\cdots, \mathbf{y}_{t-1}, \mathcal{X}) \\ & = \text{Softmax}\left( \mathbf{W_y}\mathbf{s}_t + \mathbf{b_y} \right) \\ \mathbf{s}_t & = \tanh(\mathbf{W_{ys}}\mathbf{y}_{t-1} + \mathbf{W_{ss}}\mathbf{s}_{t-1} + \mathbf{b_s}) \end{align*}\] \[\begin{align*} \text{where} \ \mathbf{y}_0 & = \text{Enc}(\mathcal{X}) \\ \mathbf{s}_0 & = \mathbf{h}_{T_{\mathbf{x}}} \end{align*}\]여기서 \(\mathbf{s}_t\)는 \(t\)번째 타임 스텝의 디코더 RNN Hidden State Vector이며 \(\mathbf{y}_0\)는 인코더가 최종적으로 생성한 문장 임베딩이다. 즉, 디코더 RNN은 입력으로 이전 타임 스텝의 인코더 아웃풋을 받는 구조라고 할 수 있다. 위의 모델을 그림으로 그리면 아래와 같다.
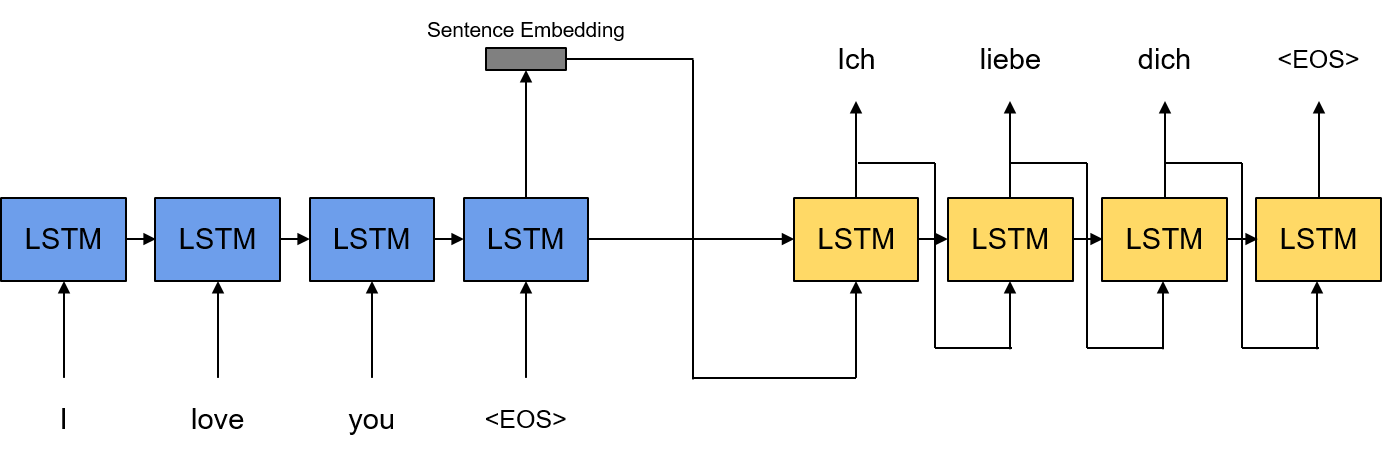
디코더의 역할은 인코더가 생성한 소스 문장의 임베딩 벡터를 이용하여 타겟 언어의 문장으로 번역된 타겟 문장을 생성하는 것이다. 그렇다면 인코더의 역할은 소스 문장을 적절한 임베딩 벡터로 변환하는 것이라고 할 수 있다. 인코더도 마찬가지로 RNN 구조를 가지고 있으며 기본적으로 문장 임베딩은 소스 문장의 마지막 입력인 <EOS>, 즉 End of Sentence가 입력된 마지막 출력 벡터를 문장 임베딩 벡터로 사용하게 된다. 또한 마지막 타임 스텝의 인코더 RNN Hidden State Vector \(\mathbf{h}_{T_{\mathbf{x}}}\)는 디코더의 첫번째 타임 스텝의 Hidden State Vector \(\mathbf{s}_0\)로 들어가게 된다.
기존 Encoder-Decoder 모델의 단점: Attention Mechanism으로 극복
이러한 기존 모델의 단점은 Bahdanau Attention 논문에서 주장하는대로 문장 임베딩을 고정된 길이로만 해야 한다는 점이다. 이 경우 짧은 문장에서는 큰 문제가 없을 수도 있지만 문장이 길어질수록 더 많은 정보를 고정된 길이로 더 많이 압축해야 하기 때문에 정보의 손실이 있다는 점이 가장 큰 문제라고 볼 수 있다. 추가적으로 RNN 특유의 Long Term Dependency 문제가 발생할 수도 있겠지만 이건 인코더 RNN을 Bidirectional로 구성하면 해결할 수 있는 문제라 여기서는 따로 언급하지 않도록 하겠다.
어쨌든 결과적으로 Attention 메커니즘을 통한 보완이 가능하다고 주장한다. Attention 메커니즘을 이용하면 인코더가 고정된 길이의 문장 임베딩을 할 필요가 없으며 소스 문장의 벡터의 시퀀스를 이용하여 디코더가 디코딩이 가능하게 된다. 따라서 문장의 길이에 관계없이 Dynamic하게 정보를 인코딩이 가능하게 된다. Attention 메커니즘을 이용하여 확률 모델 \(\widehat{\mathbf{y}}\)를 기본 RNN 모델을 이용하여 모델링하면 아래와 같다.
\[\begin{align*} \widehat{\mathbf{y}} & = p(\mathbf{y}_t \vert \mathbf{y}_0,\cdots, \mathbf{y}_{t-1}, \mathcal{X}) \\ & = \text{Softmax}\left( \mathbf{W_y}\mathbf{s}_t + \mathbf{b_y} \right) \\ \mathbf{s}_t & = \tanh(\mathbf{W_{ys}}\mathbf{y}_{t-1} + \mathbf{W_{ss}}\mathbf{s}_{t-1} + \mathbf{W_{cs}}\mathbf{c}_t + \mathbf{b_s}) \end{align*}\] \[\begin{align*} \text{where} \ \mathbf{y}_0 & = \text{<Go> Token}, \\ \mathbf{s}_0 & = \mathbf{0}, \\ \mathbf{c}_t & = \text{Attn}(\mathbf{s}_{t-1}, \mathbf{H}), \\ \mathbf{H} & = [\mathbf{h}_{1}; \cdots ; \mathbf{h}_{T_{\mathbf{x}}}] \in \mathbb{R}^{d \times T_{\mathbf{x}}} \end{align*}\]\(d\)는 인코더 RNN Hidden State Vector의 Dimension이다. 여기서 달라진 점은 \(\mathbf{y}_0\)와 \(\mathbf{s}_0\), 그리고 새롭게 Context Vector \(\mathbf{c}_t\)가 추가된 것들을 확인할 수 있다. \(\mathbf{y}_0\)는 기존과 다르게 문장 임베딩을 사용하지 않고 문장의 시작점을 나타내는 새로운 <Go> 토큰을 사용하게 되며 \(\mathbf{s}_0\)는 평범한 RNN처럼 Zero Vector를 사용하게 된다. 여기서 핵심은 \(\mathbf{c}_t\)를 어떻게 구하며 또 활용할 것이냐가 될 것이다. 방금까지의 설명을 그림으로 정리하면 아래와 같다.
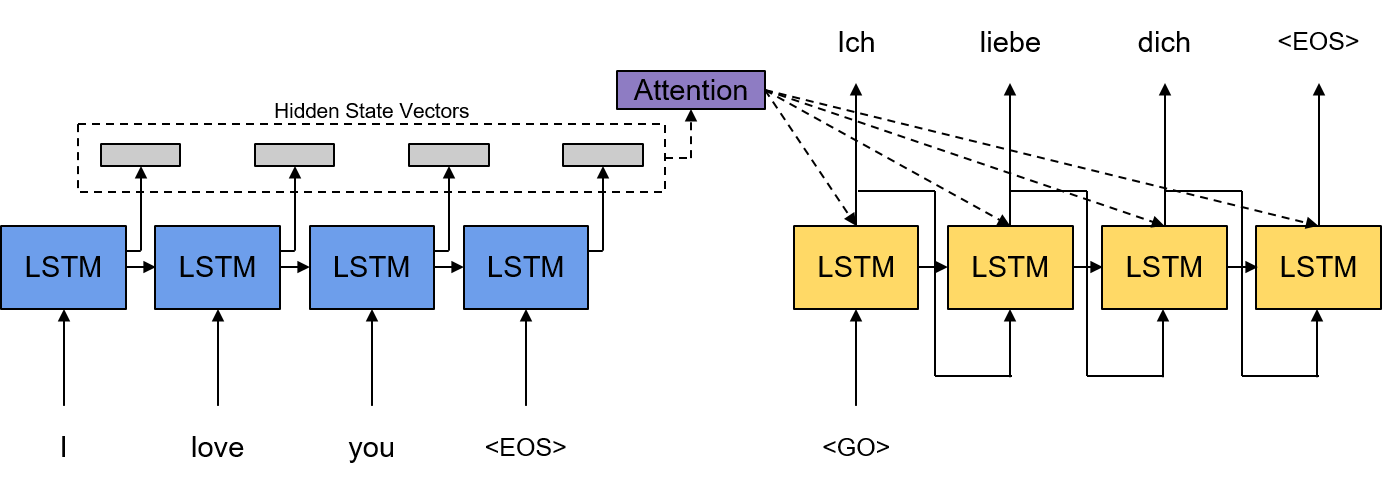
Bahdanau Attention
일단 \(\mathbf{c}_t\)를 구하는 연산이 바로 Attention 메커니즘이 수행하는 일이 될 것이다. Bahdanau Attention에서 \(\mathbf{c}_t\)는 다음과 같이 구할 수 있다.
\[\begin{align*} \mathbf{c}_t & = \sum_{j=1}^{T_{\mathbf{x}}} \mathbf{a}_{tj}\mathbf{h}_j \\ & = \mathbf{H} \mathbf{a}_t \\ \mathbf{a}_t & = \text{Softmax}\left(\left(\text{Score}(\mathbf{s}_{t-1}, \mathbf{h}_j)\right)_{j=1}^{T_{\mathbf{x}}}\right) \in \mathbb{R}^{T_{\mathbf{x}}} \\ \text{Score}(\mathbf{s}_{t-1}, \mathbf{h}_j) & = \mathbf{v}^\text{T}\tanh (\mathbf{W_a}\mathbf{s}_{t-1} + \mathbf{U_a}\mathbf{h}_j) \end{align*}\]\(\mathbf{a}_t\)는 Alignment Vector라고 정의한다. \(\mathbf{a}_t\)의 각 성분 \(\mathbf{a}_{t1}, \cdots, \mathbf{a}_{tT_{\mathbf{x}}}\)를 이용하여 \(\mathbf{h}_1,\cdots \mathbf{h}_{T_{\mathbf{x}}}\)를 Weighted Sum을 한 것이 Context Vector \(\mathbf{c}_t\)가 되는 것이다. 여기서 주의깊게 살펴봐야 하는 것이 \(\mathbf{a}_t\)의 각 성분 \(\mathbf{a}_{tj}\)는 \(\mathbf{s}_{t-1}\)과 \(\mathbf{h}_j\) 사이의 연관성을 Scoring한 결과라고 볼 수 있다. 즉, \(\mathbf{s}_{t-1}\)과 모든 \(\mathbf{h}_1,\cdots \mathbf{h}_{T_{\mathbf{x}}}\) 사이의 연관성을 Weight로 하여서 \(\mathbf{h}_1,\cdots \mathbf{h}_{T_{\mathbf{x}}}\)의 Weighted Sum을 구하는 방식으로 Context Vector를 구하는 것이다.
또 주의깊게 봐야 할 부분은 Score Function의 형태이다. 사실 두 벡터 \(\mathbf{s}_{t-1}\)과 \(\mathbf{h}_j\) 사이의 Similarity를 구한다는 관점에서 봤을 경우 \(\mathbf{W_a}\mathbf{s}_{t-1} - \mathbf{U_a}\mathbf{h}_j\)라고 쓰는 것이 더 직관적일 것 같기는 하다. \(\mathbf{W_a}\)와 \(\mathbf{U_a}\)라는 두 Linear Transformation을 통해서 임베딩 공간에 뿌려진 두 벡터 \(\mathbf{W_a}\mathbf{s}_{t-1}\)과 \(\mathbf{U_a}\mathbf{h}_j\) 사이의 거리를 \(\mathbf{W_a}\mathbf{s}_{t-1} - \mathbf{U_a}\mathbf{h}_j\)라고 정의할 수도 있기 때문이다. 어쨌든 그건 부호의 차이일 뿐이니 여기서는 큰 의미는 없다. 어쨌든 Score Function에 관해서는 Luong Attention에서 더 논하기 때문에 여기서는 넘어가도록 한다. Luong Attention에 대한 포스팅은 링크를 참조하면 된다.
GRU 모델에서의 Attention 메커니즘 활용
위에서는 기본 RNN 모델을 이용하여 확률 모델 \(\widehat{\mathbf{y}}_t\)를 모델링한 결과를 보였다. 하지만 최근에는 LSTM, GRU 등의 RNN 모델들을 활용하는 경우가 많으며 이에따라 논문 Appendix에는 GRU에 대한 Attention 메커니즘의 활용이 잘 정리가 되어있다.
먼저 기본 GRU의 연산은 아래와 같이 정리할 수 있다.
\[\begin{align*} \widehat{\mathbf{y}}_t & = \text{Softmax}\left( \mathbf{W_y}\mathbf{s}_t + \mathbf{b_y} \right) \\ \mathbf{s}_t & = \mathbf{z}_t \odot \mathbf{s}_{t-1} + (1-\mathbf{z}_t) \odot \tilde{\mathbf{s}}_t \\ \mathbf{z}_t & = \sigma(\mathbf{W_z}\mathbf{y}_{t-1} + \mathbf{U_z}\mathbf{s}_{t-1} + \mathbf{b}_z) \\ \mathbf{r}_t & = \sigma(\mathbf{W_r}\mathbf{y}_{t-1} + \mathbf{U_r}\mathbf{s}_{t-1} + \mathbf{b}_r) \\ \tilde{\mathbf{s}}_t & = \tanh(\mathbf{W_s}\mathbf{y}_{t-1} + \mathbf{U_s}(\mathbf{r}_t \odot \mathbf{s}_{t-1}) + \mathbf{b}_s) \end{align*}\]\(\sigma\)는 Sigmoid Function을 나타낸 것이다. Attention 메커니즘을 활용하여 위의 연산들을 재정의하면 아래와 같이 정리할 수 있다.
\[\begin{align*} \widehat{\mathbf{y}}_t & = \text{Softmax}\left( \mathbf{W_y}\mathbf{s}_t + \mathbf{b_y} \right) \\ \mathbf{s}_t & = \mathbf{z}_t \odot \mathbf{s}_{t-1} + (1-\mathbf{z}_t) \odot \tilde{\mathbf{s}}_t \\ \mathbf{z}_t & = \sigma(\mathbf{W_z}\mathbf{y}_{t-1} + \mathbf{U_z}\mathbf{s}_{t-1} + \mathbf{C_z}\mathbf{c}_t + \mathbf{b}_z) \\ \mathbf{r}_t & = \sigma(\mathbf{W_r}\mathbf{y}_{t-1} + \mathbf{U_r}\mathbf{s}_{t-1} + \mathbf{C_r}\mathbf{c}_t + \mathbf{b}_r) \\ \tilde{\mathbf{s}}_t & = \tanh(\mathbf{W_s}\mathbf{y}_{t-1} + \mathbf{U_s}(\mathbf{r}_t \odot \mathbf{s}_{t-1}) + \mathbf{C_s}\mathbf{c}_t + \mathbf{b}_s) \end{align*}\]GRU 모델 및 기본 RNN 모델에서의 Context Vector의 활용을 살펴보면 다음의 특징을 파악할 수 있다. Context Vector \(\mathbf{c}_t\)는 RNN의 입력으로 사용되는 \(\mathbf{y}_{t-1}\)과 함께 등장하며 함께 임베딩 공간에 뿌려져서 더해지는 방식으로 활용된다. 즉, 간단하게 정리하자면 \(\mathbf{Wy}_{t-1}\) 대신 \(\mathbf{Wy}_{t-1} + \mathbf{Cc}_t\)가 된다는 것이다. 이건 RNN 입력을 \(\mathbf{y}_{t-1}\) 단독으로 사용하는 것이 아니라 Context Vector \(\mathbf{c}_t\)와 Concatenation하여 사용하는 것과 같은 의미이다. 이걸 수식으로 정리하면 다음과 같다.
\[\begin{align*} [\mathbf{W};\mathbf{C}][\mathbf{y}_{t-1}^{\text{T}};\mathbf{c}_t^{\text{T}}]^{\text{T}} = \mathbf{Wy}_{t-1} + \mathbf{Cc}_t \end{align*}\]이 부분은 TensorFlow의 AttentionWrapper 모듈에서도 확인할 수 있는 부분이다. AttentionWrapper 모듈은 cell_input_fn을 인자로 받아 RNN의 입력 및 Attention을 어떻게 받게 할지를 설정할 수 있다. 이 때 cell_input_fn의 디폴트를 살펴보면 아래와 같음을 알 수 있다.
class AttentionWrapper(rnn_cell_impl.RNNCell):
"""Wraps another `RNNCell` with attention.
"""
def __init__(
self,
cell,
attention_mechanism,
attention_layer_size=None,
alignment_history=False,
cell_input_fn=None,
output_attention=True,
initial_cell_state=None,
name=None,
attention_layer=None
):
... (생략)
Args:
... (생략)
cell_input_fn: (optional) A `callable`. The default is:
`lambda inputs, attention: array_ops.concat([inputs, attention], -1)`.
... (생략)
즉, 현재 입력 및 Attention, 즉 여기서는 Context Vector \(\mathbf{c}_t\)가 Concatenation되어서 입력으로 사용된다는 것을 확인할 수 있다.
TensorFlow에서의 Bahdanau Attention의 활용
이 부분은 Bahdanau Attention 뿐 아니라 다음에 정리할 Luong Attention 등의 여러 다른 Attention 메커니즘들에도 동일하게 적용될 수 있는 부분이다. 기본적으로 TensorFlow에서는 Bahdanau Attention 등의 잘 알려져있는 Attention 메커니즘을 위한 모듈을 제공한다.
아래의 코드는 아주 기본적으로 활용될 수 있는 Attention 메커니즘 구현 예제이다.
import tensorflow as tf
import hyparams as hp
enc_outs = encoder(inputs)
cell = tf.nn.rnn_cell.GRUCell(num_units=hp.attention_units)
attn_mechanism = tf.contrib.seq2seq.BahdanauAttention(
num_units=hp.attention_depth, memory=enc_outs)
attn_cell = tf.contrib.seq2seq.AttentionWrapper(
cell=attn_cell, attention_mechanism=attention_mechanism,
alignment_history=True, output_attention=False)
위의 예제에서는 인코더의 RNN Hidden State Vector가 아닌 단순하게 인코더의 출력을 Attention의 입력인 Attention Memory로 설정하였다. 따라서 인코더의 출력인 enc_outs가 미리 준비되어 있어야 한다. 이제 Attention을 위한 GRU 셀을 tf.nn.rnn_cell.GRUCell을 이용하여 선언하여 준다. 위의 예제에서는 cell이 그 역할을 하게 될 것이다.
그 다음으로는 Attention 메커니즘을 선언하여야 한다. 여기서는 Bahdanau Attention을 사용하기 위하여 tf.contrib.seq2seq.BahdanauAttention 모듈을 이용하였다.
마지막으로 cell과 Attention 메커니즘인 attn_mechanism을 이용하여 Attention 셀로 묶어줘야 한다. 이 역할은 tf.contrib.seq2seq.AttentionWrapper가 담당하게 된다. 이런식으로 선언된 AttentionWrapper는 방금 더 위에서 확인할 수 있듯이 rnn_cell_impl.RNNCell을 상속받는 클래스이다. 따라서 이제 attn_cell은 기존 GRU 셀처럼 dynamic_rnn, dynamic_decode 등에 활용할 수 있게 된다.
실험 및 성능 검증
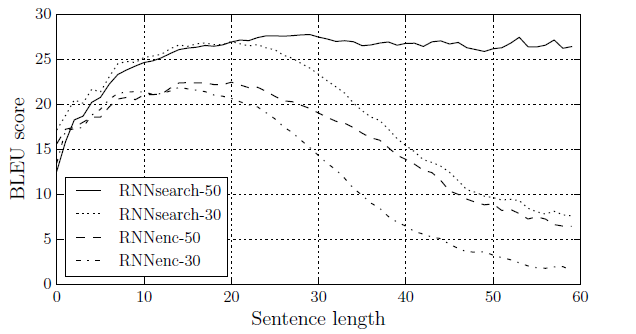
논문에서는 여러 실험을 통해서 성능을 검증하였지만 여기서는 간단하게 한가지만 소개하도록 하겠다. 실험은 기계 번역 성능을 확인하는 방식으로 진행되었다. 기본적으로 영어에서 불어로 번역하는 기능을 학습시켰는데 학습에 사용한 데이터는 ACL WMT 14에서 제공하는 데이터셋을 이용하였다. 이 데이터셋의 특징은 Bilingual하고 Parallel한 코퍼스라는 특징이 있다. 다음은 실험 결과 그래프이다.
기본적으로 BLEU 스코어를 이용하여 성능을 검증하였는데 BLEU 스코어에 대한 정리는 다음에 하도록 하겠다. 어쨌든 Attention 메커니즘을 활용한 모델인 RNNsearch-50, RNNsearch-30이 그렇지 않은 모델인 RNNenc-50, RNNenc-30 보다 성능적으로 우수하다는 점을 확인할 수 있다. RNNsearch-50, RNNenc-50은 문장 길이가 50정도 되는 코퍼스에 학습시킨 모델이고 RNNsearch-30, RNNenc-30은 마찬가지로 문장 길이가 30정도 되는 코퍼스에 학습시킨 모델이다. 또한 확실히 문장 길이가 길어질수록 성능이 떨어지는 점도 추가적으로 확인할 수 있다.
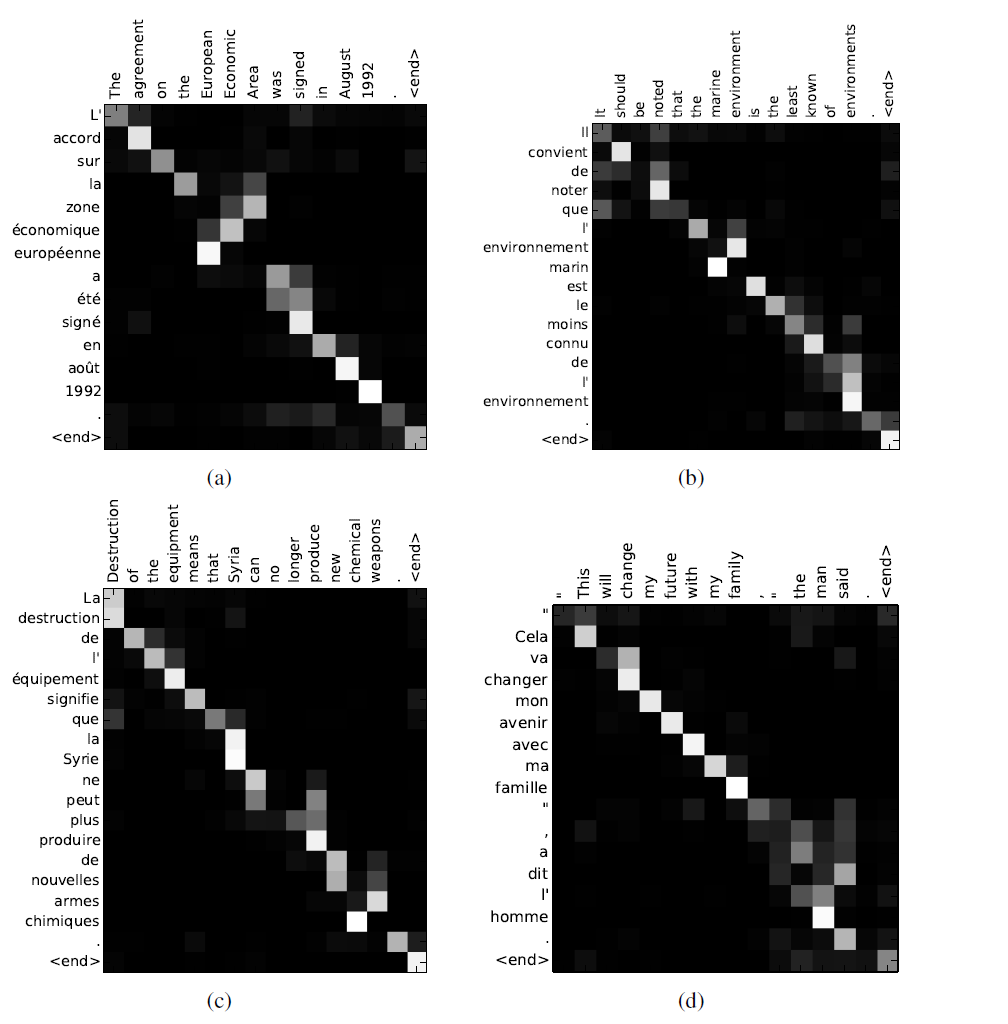
위 그림은 Attention Alignment를 시각화한 그림이다. 특정 단어를 번역하기 위해서는 그 단어에 가장 눈에 띄는 Alignment가 있어야 하며 잘 동작하는 것을 확인할 수 있다.