#knowledge tracing #deep learning #recommender system

이번 포스팅은 다음의 논문을 스터디하여 정리하였다:

Knowledge Tracing

Knowledge Tracing이란 주어진 문제들을 풀어가는 사용자의 수준을 파악하기 위한 학습 모델을 추정하기 위한 태스크를 말한다. 기존 고전 방법론으로는 Bayesian Network 및 확률 모델 파라미터 추정 방법론들을 활용한 Bayesian Knowledge Tracing (BKT)을 중심으로 연구가 되어왔으며, 현재는 딥러닝 기술을 활용하여 Deep Knowledge Tracing (DKT)을 중심으로 다양한 모델들에 대한 연구가 수행되고 있다.

이번 포스트에서 소개하고자 하는 논문은 딥러닝 기반의 Knowledge Tracing 모델이며 Dynamic Key-Value Memory Network (DKVMN)라고 불리우는 모델이다. 논문에서는 DKVMN의 우수성을 강조하기 위하여 추가적으로 Memory-Augmented Neural Network (MANN)도 제시하였지만 이번 포스트에서는 DKVMN만을 설명하도록 하겠다. (추후 MANN에 대한 설명을 추가할 예정)

또한 Knowledge Tracing에 대한 전반적인 문제 정의에 대해서는 링크를 참고하면 도움이 될 것이다.

문제 정의

DKVMN은 Knowledge Tracing 연구에서 (필자가 알기로는) 최초로 다양한 개념이 존재하고 그 개념들 사이에 상호작용을 통해서 사용자의 학습 활동이 수행된다는 점을 주장하였다. DKVMN에서 제시한 문제 세팅을 간단히 요약하면 아래의 그림과 같다.

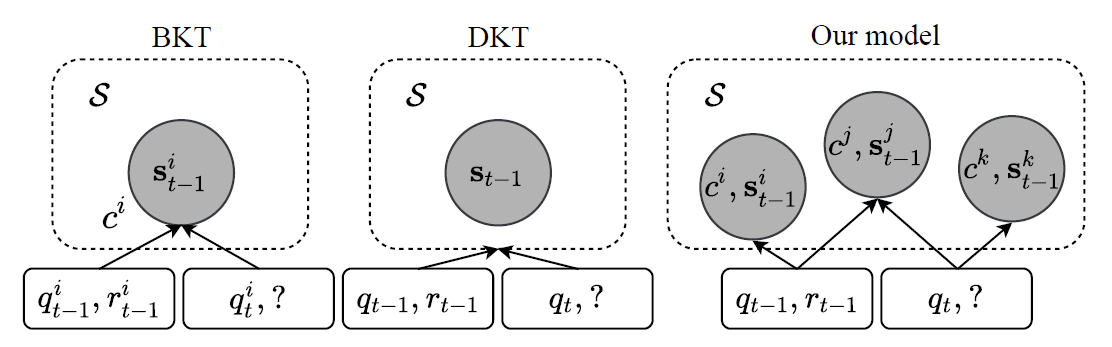
즉, BKT는 사용자와 개념들 각각마다 확률 모델을 가정하고 현상을 설명하기위한 최적의 파라미터를 추정하려고 시도한다.

DKT는 개념을 따로 가정하지는 않고 사용자에 따라 반응을 예측하는 딥러닝 모델을 활용하였고 개념은 딥러닝 상에서 숨겨진 Black Box로만 존재하여 우리가 확인할 수 없다.

하지만 DKVMN은 기존의 모델들과는 다르게 다양한 개념들이 존재하고 이들 사이에는 서로 상호작용이 가능하며 그를 통해서 사용자의 반응을 추정하는 모델을 제시한다.

여기서 중요한 점은 개념을 가정했다는 것보다도 다양한 개념들 사이의 상호작용을 상정하고 모델을 구축했다는 점을 들 수 있을것 같다.

모델 구조

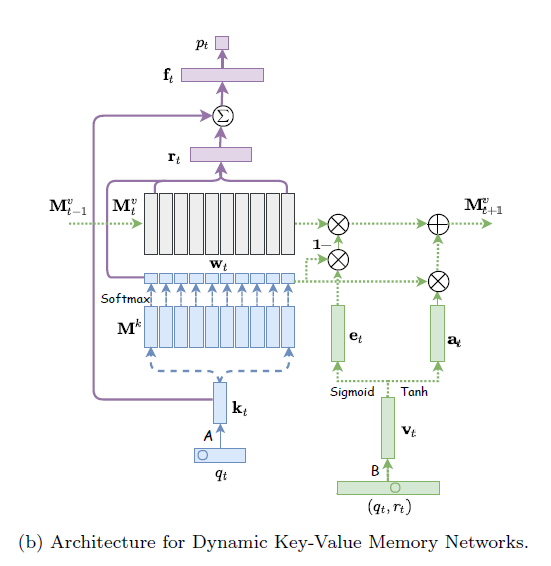
DKVMN의 모델 구조는 MANN 모델 구조에서 External Memory Matrix를 Value Matrix \(\mathbf{M}_t^v\) 및 Key Matrix \(\mathbf{M}^k\)로 나누는 방식으로 구현하였다.

Value Matrix \(\mathbf{M}^v_t\)는 \(d_v\times N\)의 크기를 가지고 있으며 \(N\)개의 Latent Concept들 \(\{ c^1, c^2, \cdots, c^N \}\) 각각에 대한 사용자의 Concept State \(\{ \mathbf{s}_t^1, \mathbf{s}_t^2, \cdots, \mathbf{s}_t^N \}\)을 인코딩하고 있다. 밑첨자 \(t\)가 들어있는 이유는 모델의 추론 과정에서 이 메모리 값들은 시간에 따라서 동적으로(Dynamic) 변화한다는 의미이며 이것이 DKVMN의 이름을 가지게 된 이유라고 볼 수 있다.

반면 Key Matrix \(\mathbf{M}^k\)는 \(N\)개의 Latent Concept들 \(\{ c^1, c^2, \cdots, c^N \}\)을 인코딩하고 있는 행렬이며 모델의 추론 과정에서 시간과 관계없이 변하지않는 Static한 메모리라고 볼 수 있다.

DKVMN 모델 추론은 크게 3단계로 구성된다. 먼저 Correlation Weight 계산, 그 다음으로 Read Process, 마지막으로 Write Process이다.

Correltation Weight

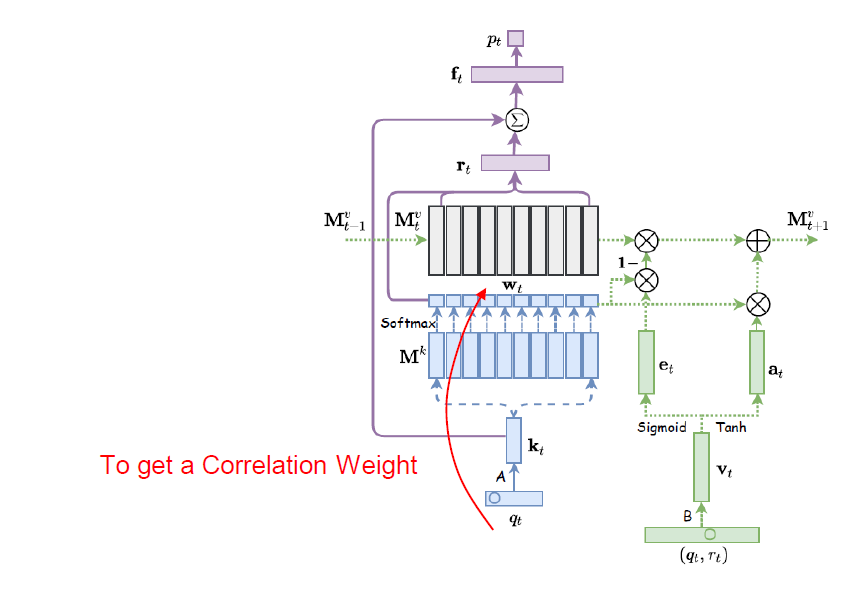
Correlation Weight 계산은 아래와 Attention Mechanism을 통해서 수행될 수 있다:

\[\mathbf{w}_t = \text{Softmax}(\mathbf{k}_t^\text{T}\mathbf{M}^k) \in \mathbb{R}^N\]

즉, 문제 인덱스 \(q_t\)의 임베딩 벡터인 \(\mathbf{k}_t\)와 Key Matrix \(\mathbf{M}^k\)의 각 열벡터들과 Attention을 통해서 \(N\)개의 Latent Concept들 \(\{ c^1, c^2, \cdots, c^N \}\) 각각과 유사도를 계산하고 Softmax를 통해서 정규화를 수행하여 Correlation Weight \(\mathbf{w}_t\)를 구하게 된다.

Read Process

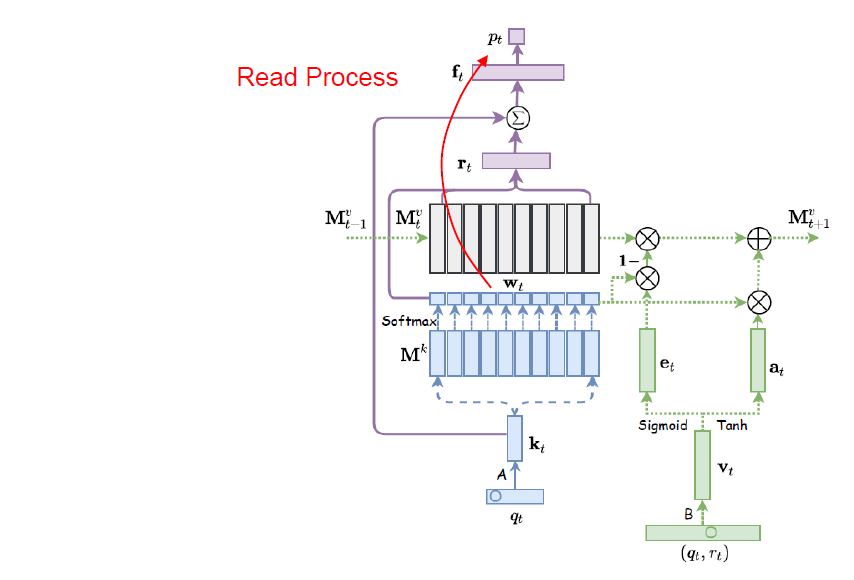
위에서 결정된 Correlation Weight \(\mathbf{w}_t\)는 Value Matrix \(\mathbf{M}^v_t\)의 각 열벡터(사용자의 Concept State)들의 Weight Sum \(\mathbf{r}_t\)를 계산하는데 Weight로 사용되게 되며 이 의미는 현재 주어진 문제 \(q_t\)에 대한 Response의 분포는 \(q_t\)와 유사한 개념에 해당하는 사용자의 Concept State의 영향을 받을 것이라는 개념을 내포하고 있다.

\[\mathbf{r}_t = \mathbf{M}^v_t\mathbf{w}_t \in \mathbb{R}^N\]

이렇게 구해진 \(\mathbf{r}_t\)는 문제 임베딩 \(\mathbf{k}_t\)와 Concat되어 Fully-Connected Layer를 거쳐 \(\mathbf{f}_t\)를 계산하게 된다.

\[\mathbf{f}_t = \text{Tanh}(\mathbf{W}_1[\mathbf{r}_t^\text{T};\mathbf{k}_t^\text{T}]^\text{T} + \mathbf{b}_1)\]

이렇게 계산된 \(\mathbf{f}_t\)는 다시 Fully-Connected Layer를 거쳐 최종적으로 Response 분포 \(p_t\)를 계산하게 된다.

\[p_t = \text{Softmax}(\mathbf{W}_2\mathbf{f}_t + \mathbf{b}_2) \in \mathbb{R}^Q\]

여기서 \(Q\)는 전체 문제의 개수이다.

Write Process

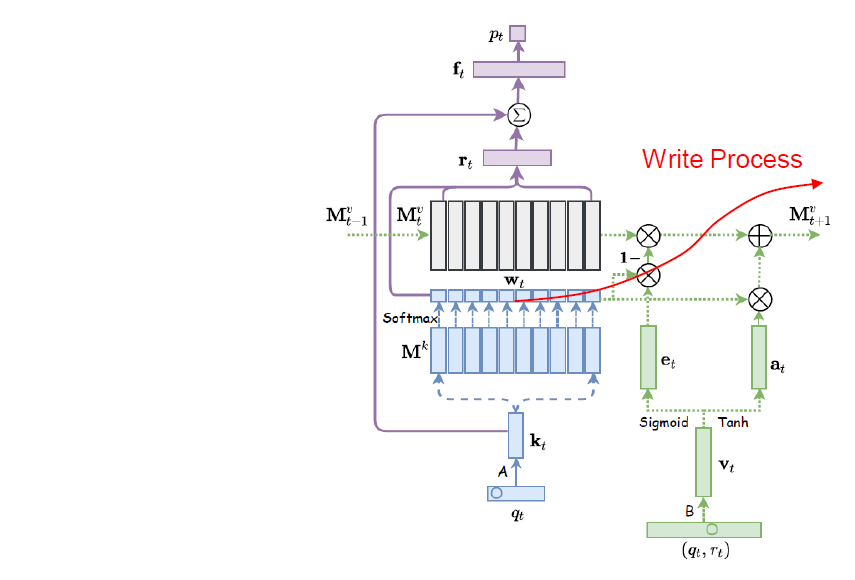
Write Process는 사용자의 상호작용 \((q_t, r_t)\)를 활용하여 현재 사용자의 Concept State를 업데이트하는 과정을 말한다.

Write Process는 Erase Vector \(\mathbf{e}_t\) 및 Add Vector \(\mathbf{a}_t\)를 먼저 구해서 Value Matrix를 업데이트하게 된다. Erase Vector 및 Add Vector를 구하기 위해서 먼저 상호작용을 \(\mathbf{v}_t\)로 임베딩하여 \(\mathbf{v}_t\)를 통해서 \(\mathbf{e}_t\) 및 \(\mathbf{a}_t\)를 구하게 된다.

\[\begin{align} \mathbf{e}_t & = \sigma(\mathbf{E}\mathbf{v}_t + \mathbf{b}_e) \\ \mathbf{a}_t & = \text{Tanh}(\mathbf{D}\mathbf{v}_t + \mathbf{b}_a) \end{align}\]

이렇게 구해진 Erase Vector 및 Add Vector를 통해서 Value Matrix는 다음과 같이 업데이트가 수행된다. 여기서 \(i\)에 대한 인덱싱은 \(i\)번째 열벡터를 의미한다.

\[\begin{align} \tilde{\mathbf{M}}_{t+1}^v(i) &= \mathbf{M}_t^v(i)[1 - w_t(i)\mathbf{e}_t] \\ \mathbf{M}_{t+1}^v(i) &= \tilde{\mathbf{M}}_{t+1}^v(i) + w_t(i)\mathbf{a}_t \end{align}\]

여기서 \(\mathbf{w}_t\)를 활용하여 주어진 문제에 해당하는 Concept State의 업데이트를 더 강하게 수행하게끔 구현했다.

Training

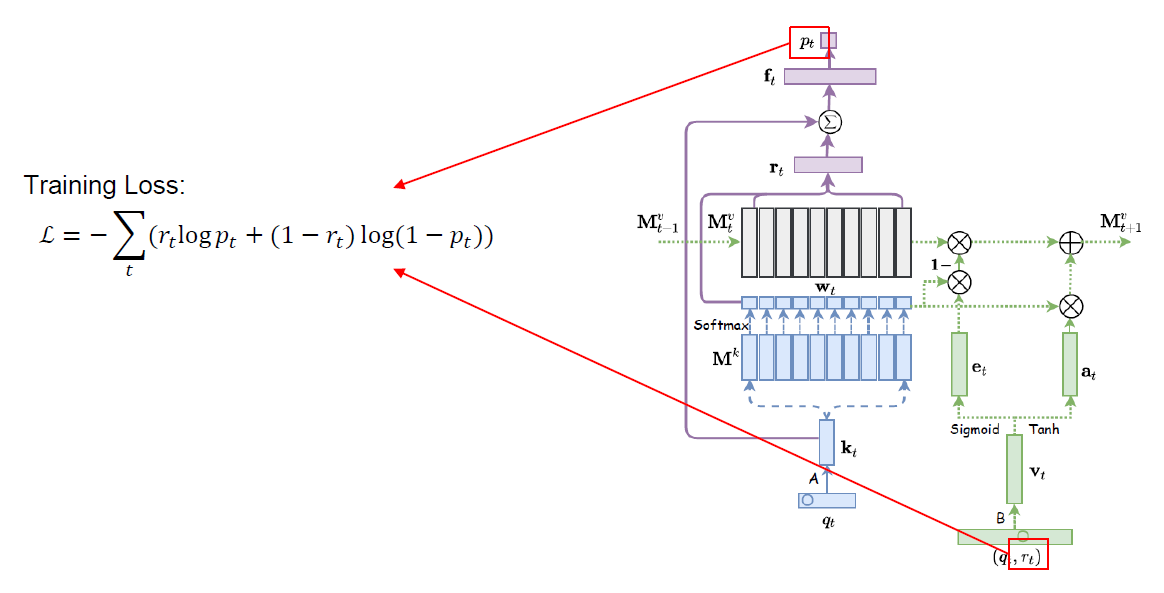
모델 학습은 위의 그림과 같이 주어진 문제 \(q_t\)에 대한 Response 분포 예측 \(p_t\)와 실제 Response 레이블 \(r_t\) 사이의 Binary Cross Entropy Loss를 최소화하는 방식을 통해서 학습이 수행된다.

\[\mathcal{L} = -\sum_t(r_t \log p_t + (1 - r_t)\log (1 - p_t))\]

특히 DKVMN 모델은 모델 전체가 미분가능하기 때문에 Stochastic Gradient Descent를 통해서 학습이 수행될 수 있다. 모델 학습에는 모멘텀을 0.9로 두고 Stochastic Gradient Descent를 수행하였으며 Gradient에 대해서는 Norm 50을 기준으로 Clipping을 수행하였다. 모든 학습용 데이터는 시간 길이를 200단위로 잘라서 전처리를 수행하였으며 200보다 짧은 데이터는 Null 값으로 패딩을 수행하였다.

저자들은 특히 학습하는 과정에서 Key Matrix 및 Initial Value Matrix 역시 학습 가능한 파라미터로 설정하고 학습을 진행하였다고 강조하고 있으며, 테스트 과정에서는 Key Matrix는 고정하였고 Initial Value Matrix는 시간이 지남에 따라서 새로운 Value Matrix로 업데이트되게끔 설정하였다고 한다.

Prediction Performance

DKVMN은 기본적으로 성능 평가를 DKT와 비교하는 방식으로 수행하였다. 데이터셋은 총 4가지를 사용하였고 각각의 상세 정보는 다음과 같다.

성능 평가는 DKT와 마찬가지로 AUC를 비교하는 방식으로 수행하였고 그 결과는 아래와 같다.

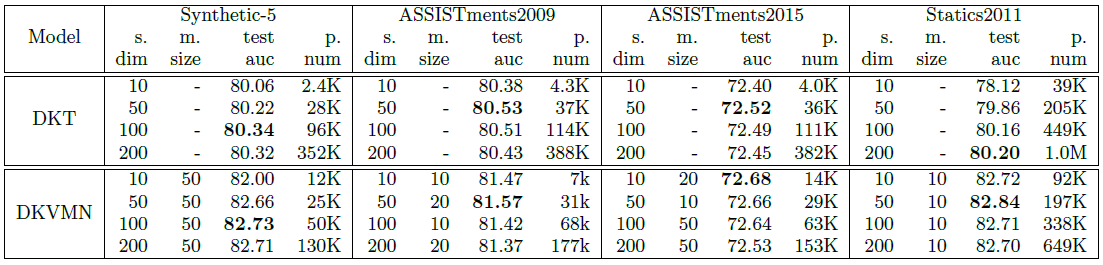
위의 결과를 통해서 저자들은 DKVMN이 DKT에 비해서 더 적은 파라미터를 가지고도 더 좋은 성능을 보인다고 주장한다.

이 부분에 대해서 개인적인 견해를 덧붙이자면, 딥러닝 모델을 모델링하는 경우 현재 모방하고자 하는 현실 모델에 대한 지식 또는 정보를 활용하여 딥러닝 모델링을 수행하는 경우에는 더 좋은 성능을 확보할 수 있다는 점을 이야기하고 싶다.

여기서 사용했던 현실 모델에 대한 지식은 모든 사용자마다 Concept State가 시간에 따른 Stochastic Process의 형태로 존재하며 각각 입력 피쳐에 대한 중간 피쳐들과의 인과관계를 최대한 활용하여 (특히, Read Process 및 Write Process에) 적용하였다는 점을 생각해볼 수 있겠다.

Concept Discovery

DKVMN 모델은 전문가의 태깅이 없이도 문제마다 내재된 개념을 찾아낼 수 있는 능력이 있다고 주장한다. 그 방법은 Correlation Weight를 이용하는 것인데 이 Correlation Weight이 가장 큰 개념에 해당하는 개념이 바로 주어진 문제에 해당하는 개념으로 결정되게 된다. 이러한 방식을 통해서 전문가가 태깅한 개념을 쉽게 찾아낼 수 있음을 아래 그림을 통해 보였다.

추가적으로 논문에서는 DKVMN의 사용자 Knowledge State를 확인하는 방법도 제시한다. 먼저 사용자의 \(i\)번째 개념에 대한 이해도를 확인하고 싶다면 먼저 Correlation Weight를 \(i\)번째의 값만을 1로 설정한 \([0, \cdots, w_i, \cdots, 0], w_i=1\) 형태의 One-Hot 벡터로 고정을 한다. 그 다음 Read Process를 통해서 먼저 \(\mathbf{r}_t\)를 구하게 된다. 이렇게 구해진 \(\mathbf{r}_t\)를 활용해서 \(\mathbf{f}_t\)를 구할때 문제에 대한 정보인 \(\mathbf{k}_t\)를 지워서 문제에 대한 정보를 무시한다.

\[\mathbf{f}_t = \text{Tanh}(\mathbf{W}_1[\mathbf{r}_t^\text{T};\mathbf{0}^\text{T}]^\text{T} + \mathbf{b}_1)\]

이렇게 구해진 \(\mathbf{f}_t\)를 활용하여 Read Process를 끝까지 진행하고 Response Prediction \(p_t\)를 구하면 이 \(p_t\)가 사용자의 \(i\)번째 개념에 대한 이해도로 활용될 수 있다고 저자들은 주장한다. 아래 그림은 이렇게 구해진 사용자 Concept Discovery 결과이다. 시간에 따라서 5개의 개념에 대한 사용자의 이해도 값이 점차 변화한다는 것을 확인할 수 있다.

기타 참고 자료

수정 사항

  • 2021.04.17
    • 최초 게시

Go back to the List of Studies