이번 포스팅은 다음의 논문을 스터디하여 정리하였다:
Knowledge Tracing
Knowledge Tracing이란 학습자의 퍼포먼스를 바탕으로 학습자의 전체 지식 수준을 평가하는 Task를 말한다. Knowledge Tracing을 적용하기 위해서 해당 모델이 가정하고 있는 몇 가지 상황에 대해서 정리해보면 다음과 같다. 먼저 활용하고자 하는 정보인 학습자 퍼포먼스는 바로 학습자가 풀어놓은 문제 풀이 결과를 말한다. 또한 평가하기 위한 지표인 학습자의 지식 수준은 학습자가 주어진 문제들을 잘 풀어낼 확률을 말하게 된다.
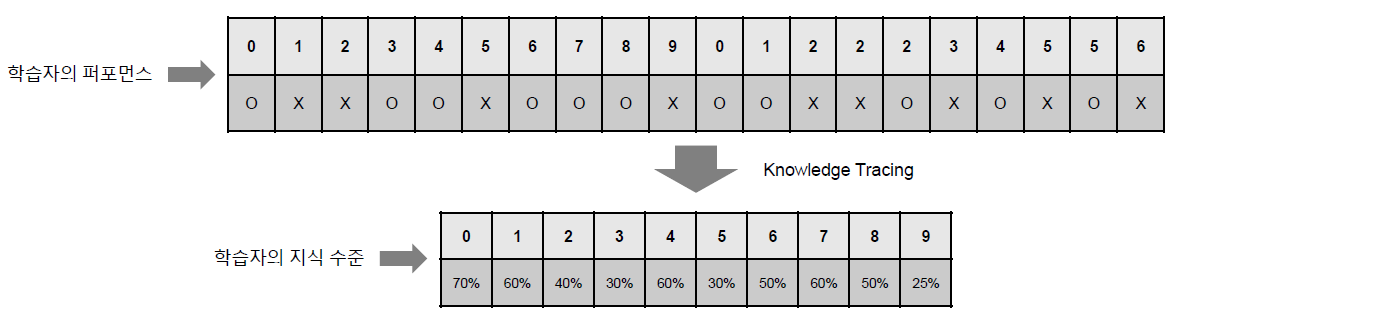
위 그림에서는 학습자의 퍼포먼스로 주어진 문제 세트에 대한 학습자의 정오답 결과가 주어지게 되며 Knowledge Tracing 모델은 이 정오답 결과를 바탕으로 학습자의 지식 수준에 해당하는 전체 문제 세트에 대한 정답률 예측 결과를 내보내게 된다.
또한 가장 중요한 가정은 바로 문제 풀이 순서에 따라서 학습자의 학습 효율이 달라질 수 있다는 점이다.
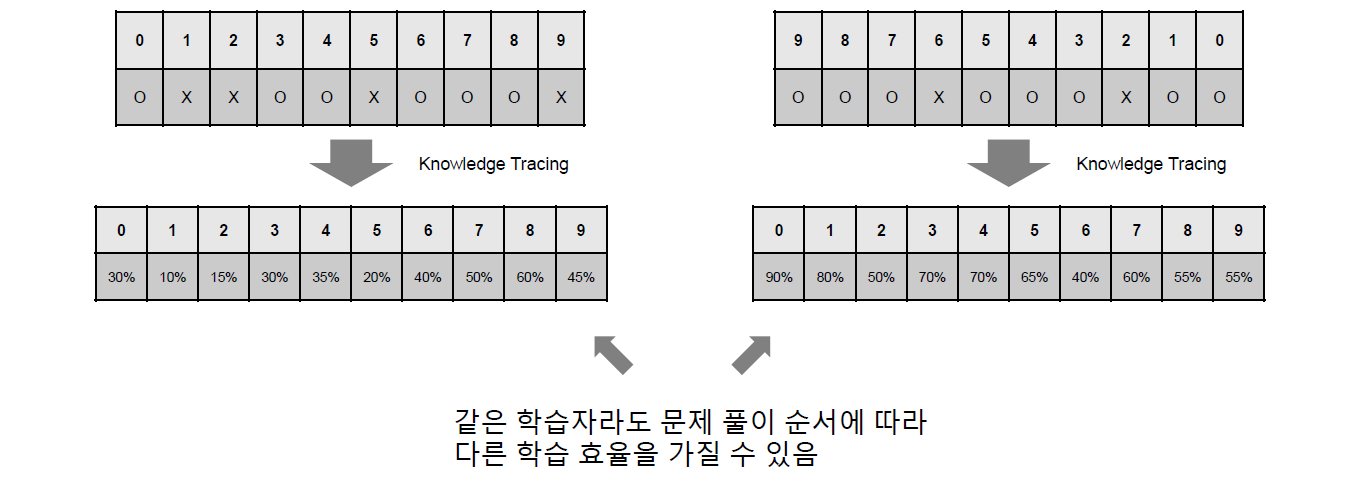
위의 그림에서와 같이 주어진 문제 세트의 순서에 따라서 학습자의 지식 수준이 달라지는 것을 확인할 수 있다. 이러한 가정들을 바탕으로 Knowledge Tracing이 수행되게 된다.
Deep Knowledge Tracing
Deep Knowledge Tracing (DKT) 모델은 처음으로 Knowledge Tracing 분야에 Deep Learning을 적용한 논문이다. 특히 RNN을 사용하였으며 추가적인 Contribution은 학습된 모델을 활용할 수 있는 Task들도 제시했다는 점을 들 수 있겠다. 그 Task들은 정리하면 아래와 같다:
- 문제 시퀀스 최적화
- 문제 사이의 연관성 정의
(Piech, Chris, et al. “Deep knowledge tracing.” Advances in neural information processing systems. 2015.)
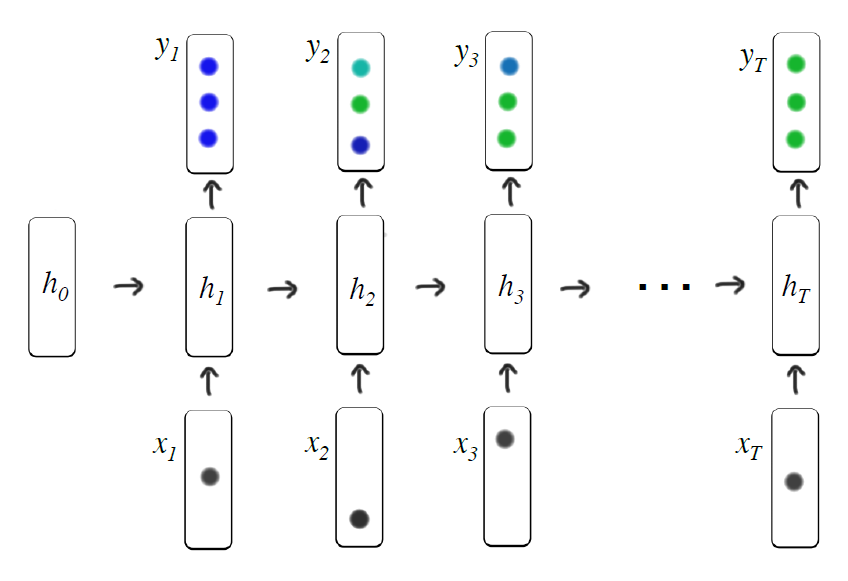
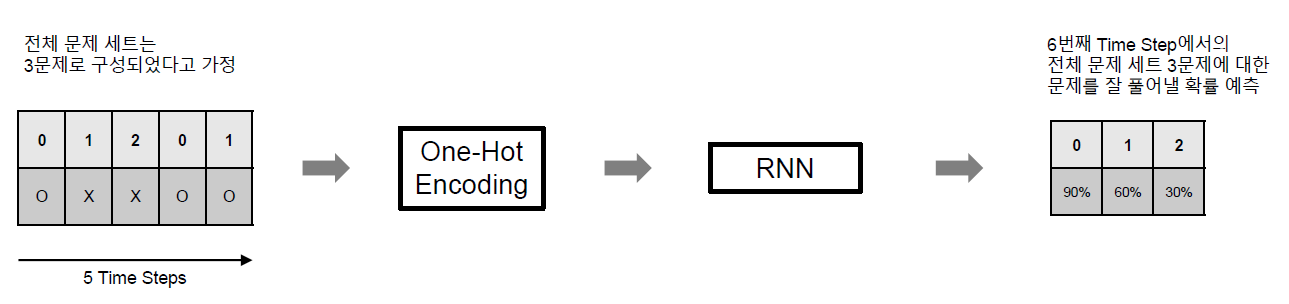
DKT 모델은 위 그림과 같은 간단한 RNN 모델로 구성되어 있다. DKT 모델은 아래와 같이 5개의 Time Step을 입력으로 받아서 6번째 Time Step에서의 전체 문제 세트 (여기서는 3문제로 구성되어 있다고 가졍) 각각에 대한 정답을 맞출 확률을 예측하게 된다.
DKT 모델을 자세히 살펴보기 위해서는 이 모델이 One-Hot Encoding과 RNN이라는 두 단계로 구성되어 있다는 점을 짚고 넘어갈 필요가 있다.
One-Hot Encoding
먼저 Knowledge Tracing에서 가장 중요한 Feature인 상호작용을 정의하고 넘어갈 필요가 있다. 전체 문제 세트가 \(M\)개라고 할 때 현재 시간 \(t\)에서의 상호작용 \(x_t=(q_t, r_t)\)는 현재 시간 \(t\)에서 학습자가 풀었던 문제 인덱스 \(q_t\)와 그 문제에 대한 학습자의 반응 \(r_t\) (학습자가 문제를 맞춘 경우 \(1\), 틀린 경우 \(0\))을 통해서 정의할 수 있다.
상호작용의 표현은 일반적으로 상호작용 인덱스를 정의하여 사용하는데, 상호작용 인덱스(\(x_t\))는 일반적으로 다음과 같이 정의할 수 있다:
\[x_t = q_t + M * r_t\]이 정의를 간단하게 설명하면 먼저 \(1\)부터 \(M\)까지의 인덱스는 반응이 \(0\)인 경우, 현재 주어진 문제가 몇 번 문제인지를, \(M+1\)부터 \(2M\)까지의 인덱스는 반응이 \(1\)인 경우, 현재 주어진 문제가 몇 번 문제인지를 나타낸다고 생각하면 될 것 같다. 이런식으로 총 \(2M\)개의 인덱스를 통해서 상호작용을 겹치는 것 없이 표현할 수 있다.
아래 그림을 통해서 예제를 살펴볼 수 있다.
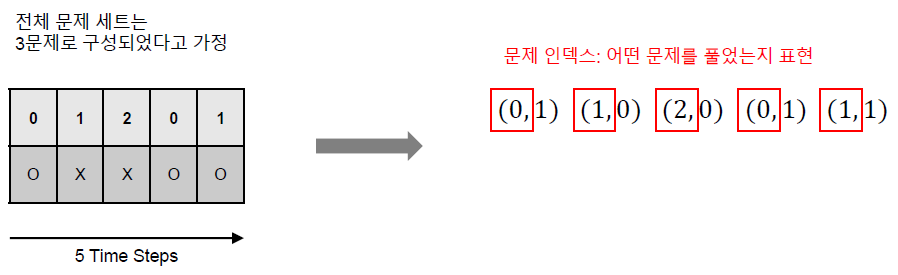
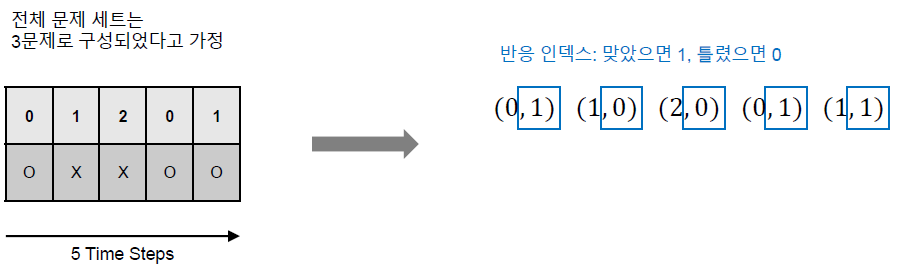
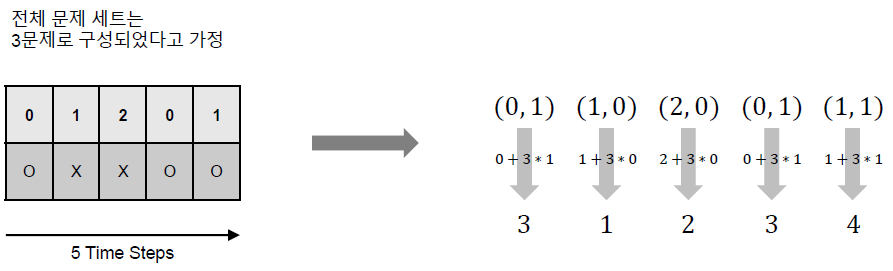
이렇게 상호작용을 인덱스로 표현한 이후 바로 One-Hot Encoding을 수행할 수 있다.
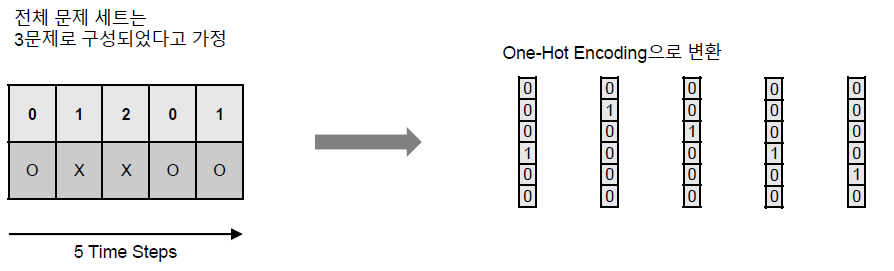
Inference
인코딩 이후에 RNN 모델의 Inference는 다음 그림과 같이 수행되게 된다. 매우 Naive한 접근이라는 것을 알 수 있다.
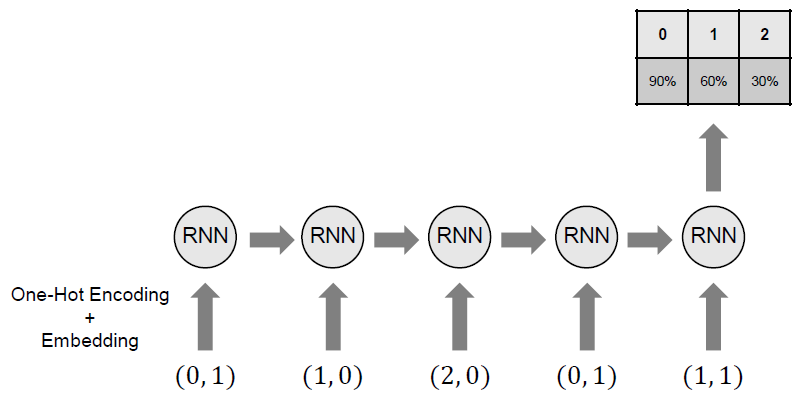
Training
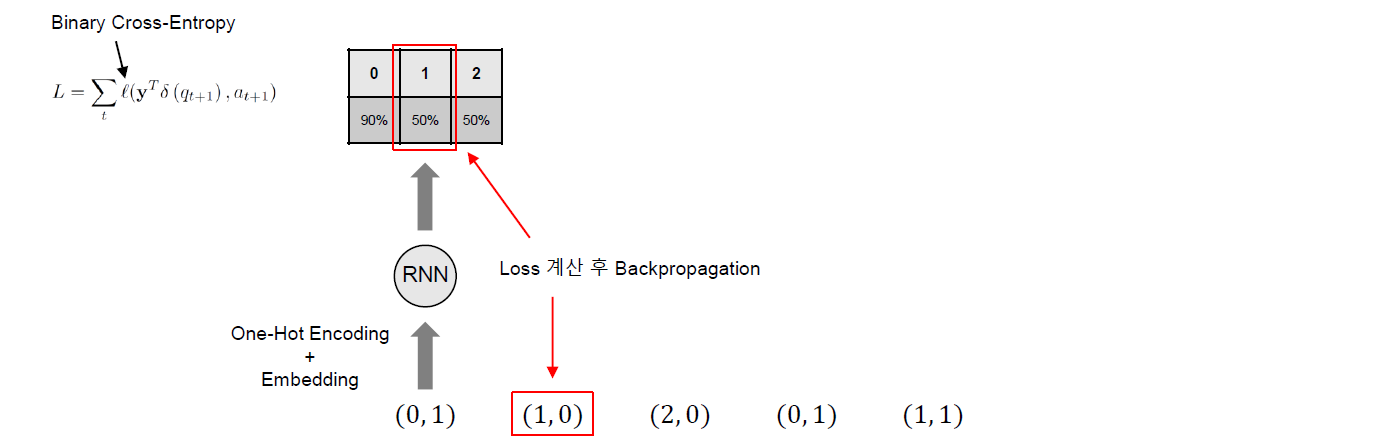
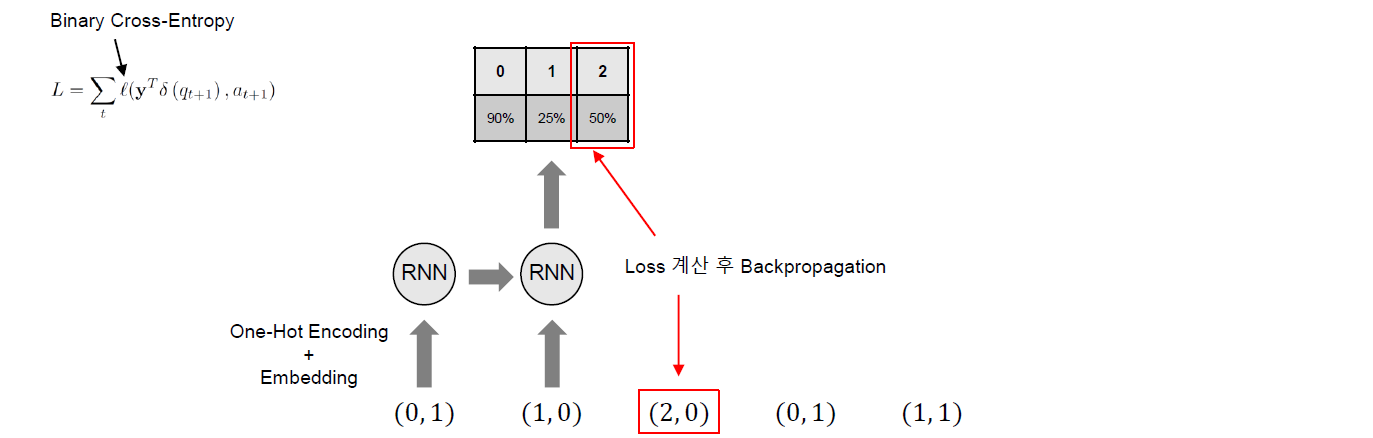
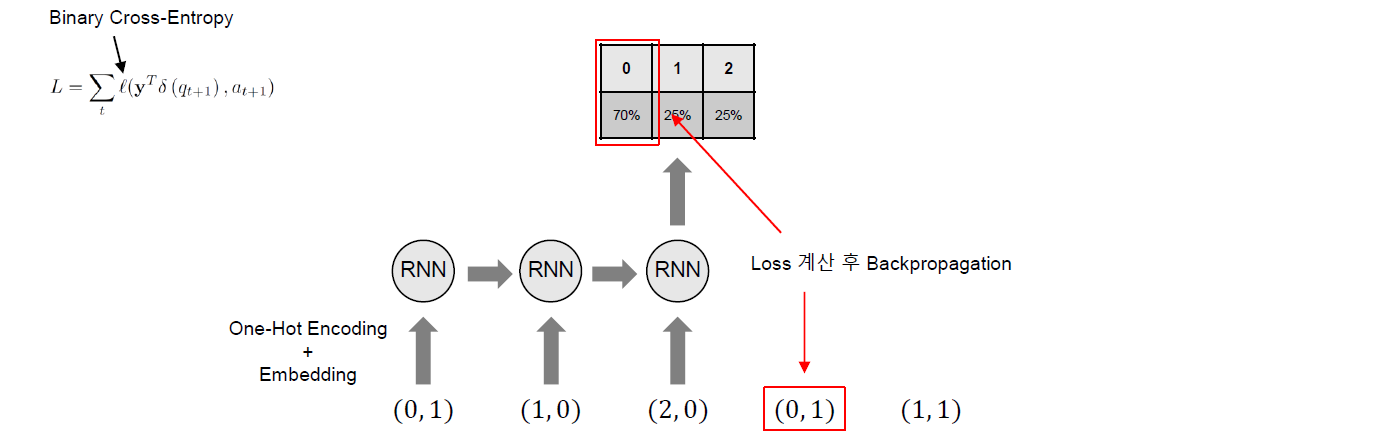
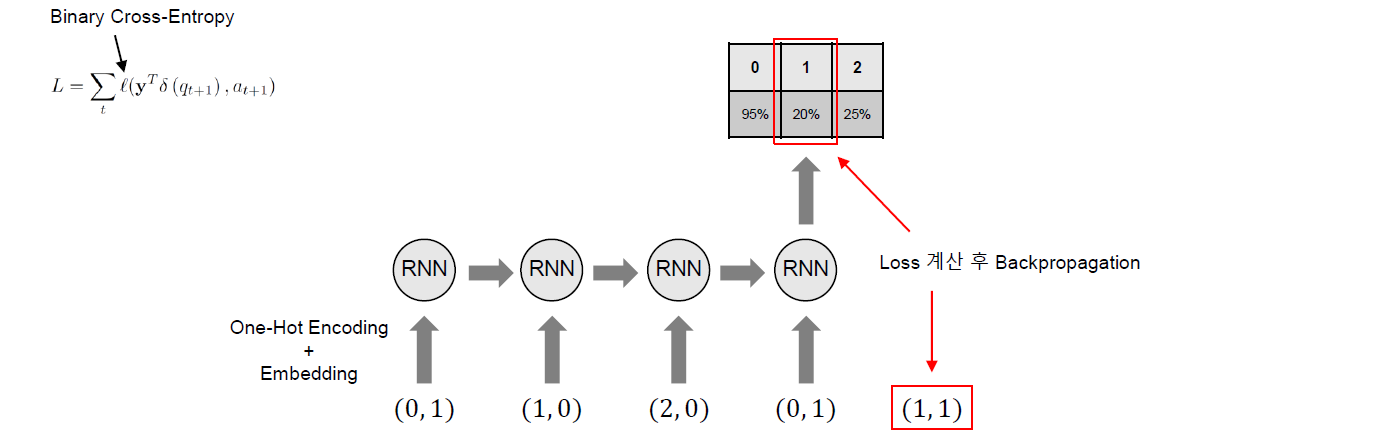
Training은 아래 그림과 같이 다음 Time Step에서 푼 문제만을 고려하여 학습의 Label로 사용하여 수행되게 된다. 이 경우 Loss Function은 아래와 같이 Binary Cross-Entropy를 사용하게 된다.
\[L = \sum_t l(\mathbf{y}^{\text{T}} \delta(q_{t+1}), a_{t+1})\]여기서 \(l\)은 Binary Cross-Entropy이며 \(\delta\)는 다음 Time Step에서 푼 문제만을 고려하여 학습의 Label로 사용하기 위한 기법이다. \(\delta\)는 One-hot 벡터이며 다음 Time Step에서 풀었던 문제의 인덱스를 표시하고 있다. 따라서 출력 \(\mathbf{y}\)와 내적을 수행하면 다음 Time Step에서 푼 문제에 대해서만 Backpropagation을 수행하게 되며 결과적으로 다음 Time Step에서 푼 문제만을 고려하여 학습이 수행되게 된다.
좀 더 자세한 이해가 필요하다면 링크를 통해 확인할 수 있는 DKT 코드를 살펴보면 도움이 될 것이다.
활용 1: 문제 시퀀스 최적화
앞서 설명했듯이 학습자는 문제를 풀면서 지식을 습득하는 과정을 거치게 된다. 이 경우 문제를 푸는 순서에 따라서 지식을 습득하는 학습의 효율이 달라진다는 점을 가정한다는 것도 앞에서 언급하였었다.
특히 이러한 문제 시퀀스 최적화는 Markov Decision Process (MDP) 문제로 변환이 가능하다.
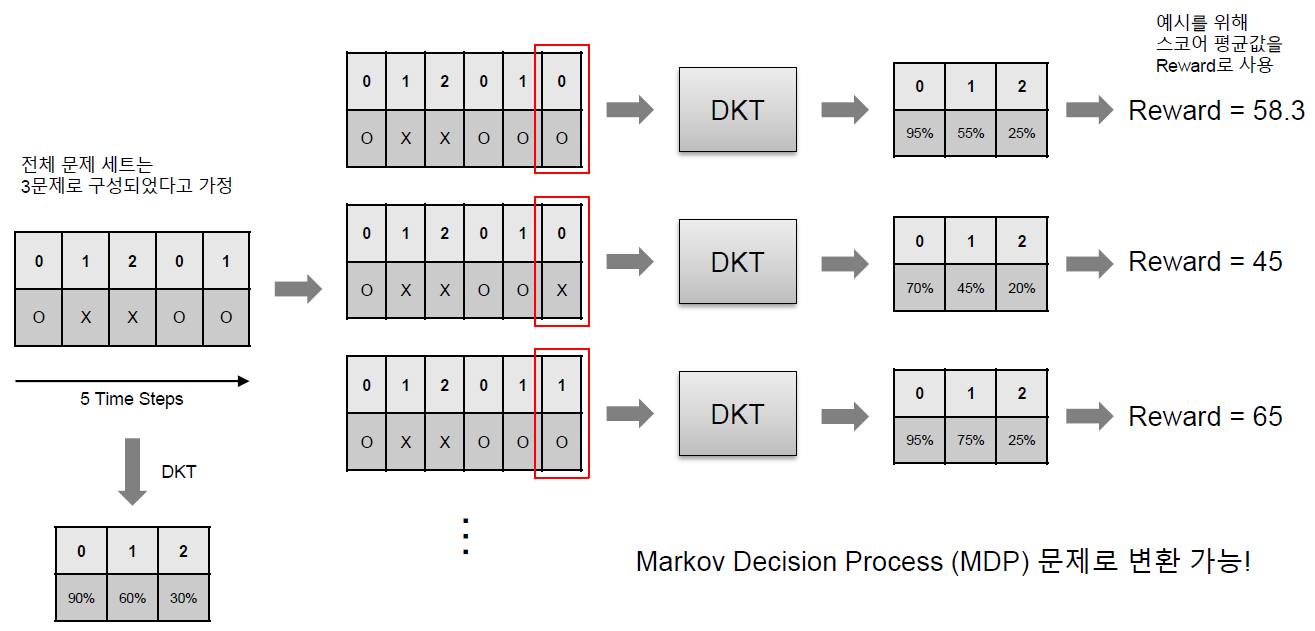
5개의 Time Step를 입력으로 받으면 6번째 Time Step에서의 문제 정답 확률을 예측할 수 있다. 이 확률 예측값들을 바탕으로 다음 Time Step, 즉, 이 예제에서는 6번째 Time Step에서 전체 문제 세트 중 어떤 문제를 풀도록 추천하는 것을 생각해볼 수 있다.
먼저 가능한 모든 문제 세트(여기서는 3문제가 될 것이다.)에 대해서 정답, 또는 오답의 경우를 모두 DKT에 입력하여 그 다음 Time Step에서의 전체 문제 세트에 대한 정답 확률을 예측한다. 이 확률 예측값들이 현재 경우의 수에 대한 Reward라고 볼 수 있다. 위의 예제에서는 간단하게 확률 예측을 스코어로 하여 스코어의 평균을 구하게 하였다.
이런 방식으로 모든 경우의 수에 대해서 Reward를 구할 수 있으며 이 상황을 Tree 구조로 바꿀 수 있을 것이다.
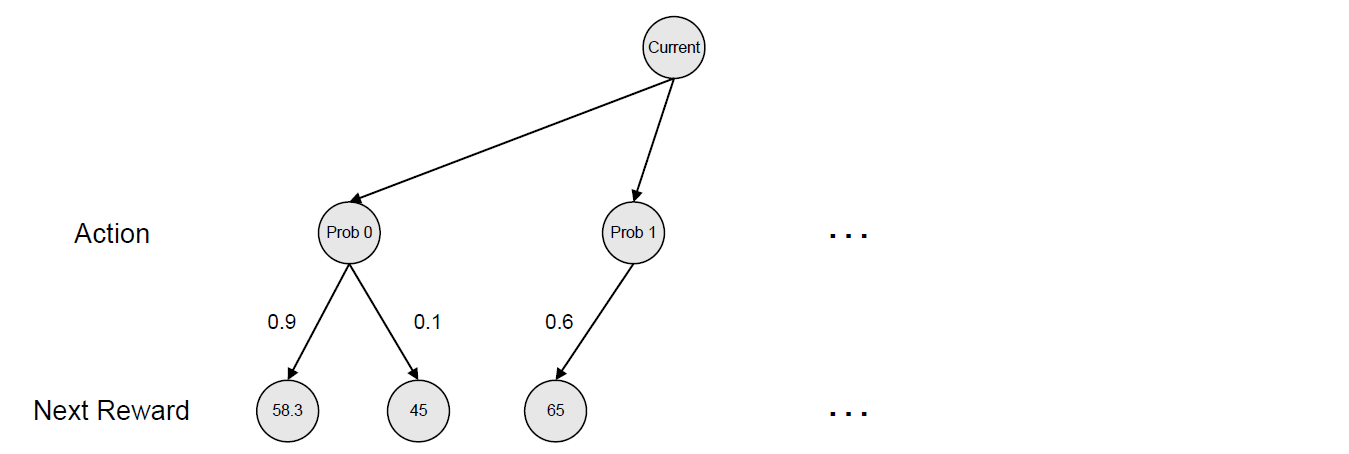
Tree는 가장 상단에 현재 State를 반영하는 Node가 존재하며 현재 Node로 부터 가능한 Action들을 그 다음 단계의 Node로 구성할 수 있다. 위의 예제에서는 총 3문제를 추천할 수 있으며 따라서 Action의 가능한 경우의 수는 3가지가 된다.
여기서 어떤 Action을 선택하는 문제는 각 Action에 대해서 얻을 수 있는 Reward가 어떻게 되는지를 살펴봄으로써 해결할 수 있을 것이다.
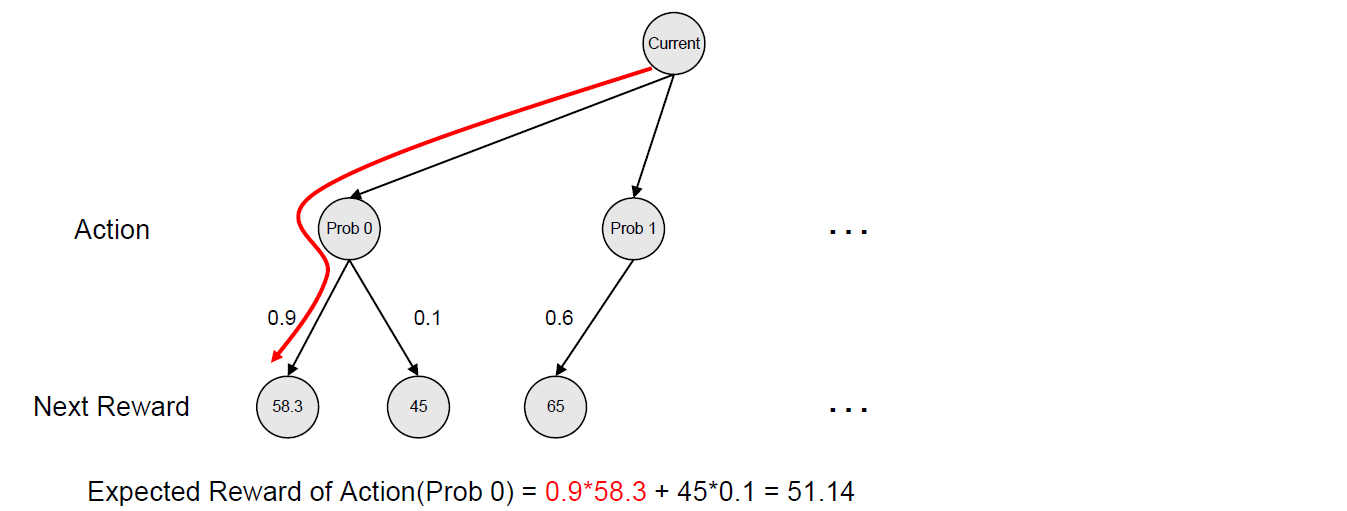
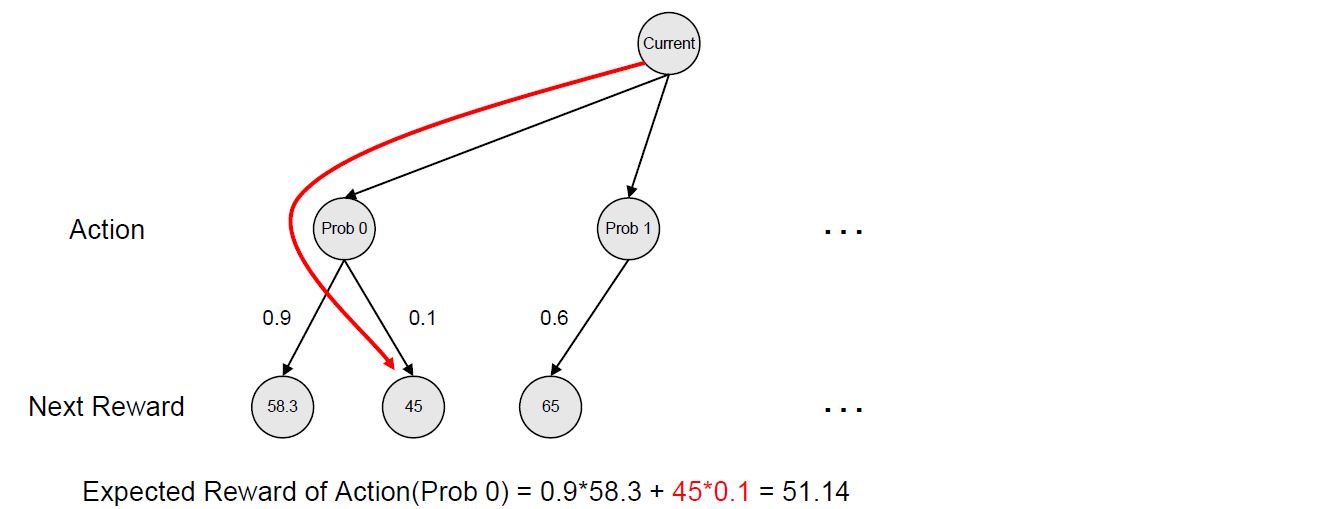
1번 문제를 추천하는 Action에 대해서는 그 다음에 얻을 수 있는 Reward로 두 가지를 고려할 수 있다. 두 가지는 맞았을 확률과 틀렸을 확률이 된다. 이 두 확률을 이용하여 Reward의 평균을 구하게 되고 이것이 1번 문제를 추천하는 Action에 대한 대표 Reward가 된다.
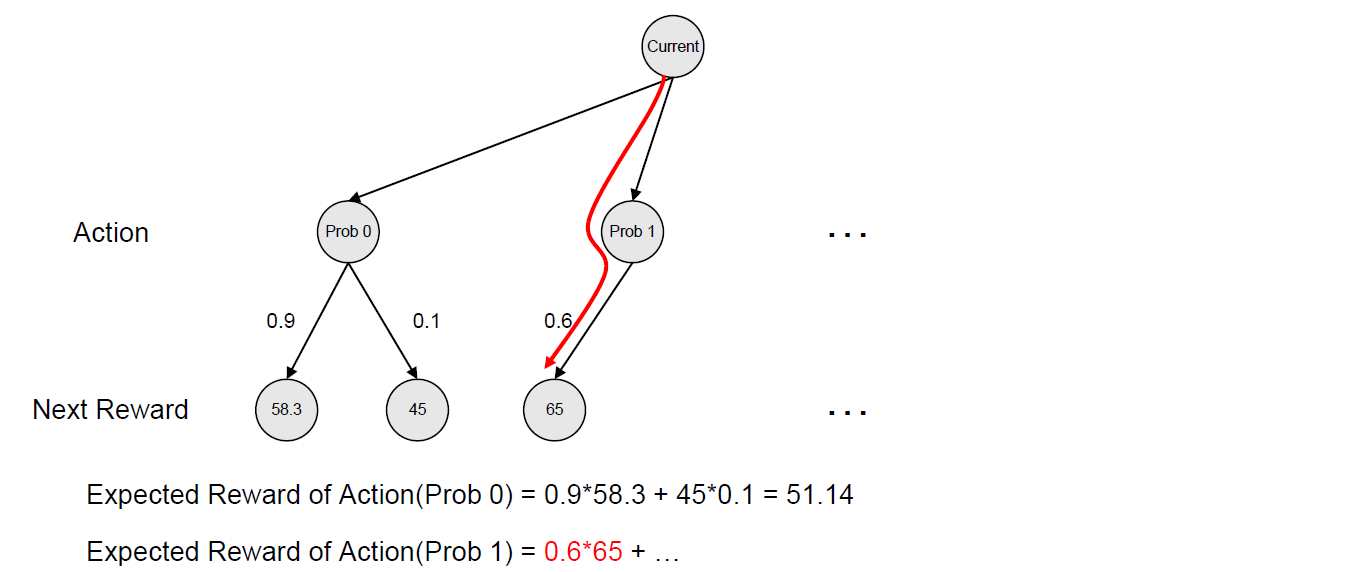
마찬가지의 방법으로 2번 문제를 추천하는 Action에 대한 대표 Reward를 구할 수 있다.
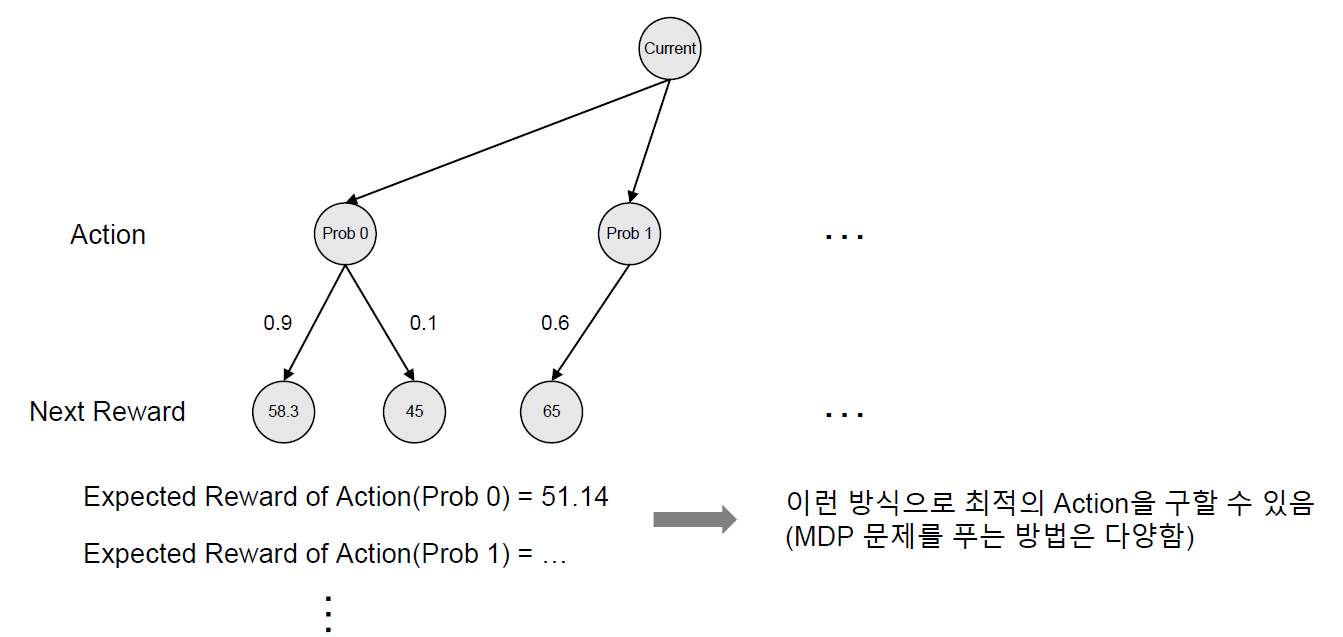
예시로 들었던 방법은 Expectimax라는 Tree Search 알고리즘이다. MDP 문제를 풀 수 있는 Tree Search 알고리즘은 Expectimax 외에 Minimax, Dynamic Programming 등 다양하다.
활용 2: 문제 사이의 연관성 정의
논문에서는 학습이 완료된 DKT 모델의 활용하여 문제 사이의 연관성을 정의할 수 있다고 주장한다. \(i\)번 문제와 \(j\)번 문제 사이의 연관성 \(J_{ij}\)는 다음과 같이 정의할 수 있다.
\[J_{ij} = \frac{y(j \vert i)}{\sum_{k}y(j \vert k)}\]여기서 \(y(j \vert i)\)는 \(i\)번 문제를 맞췄을 때 다음 Time Step에서 \(j\)번 문제를 맞출 확률로 정의한다. 다음 그림을 통해서 \(y(j \vert i)\)의 정의를 좀 더 쉽게 이해할 수 있을 것이다.
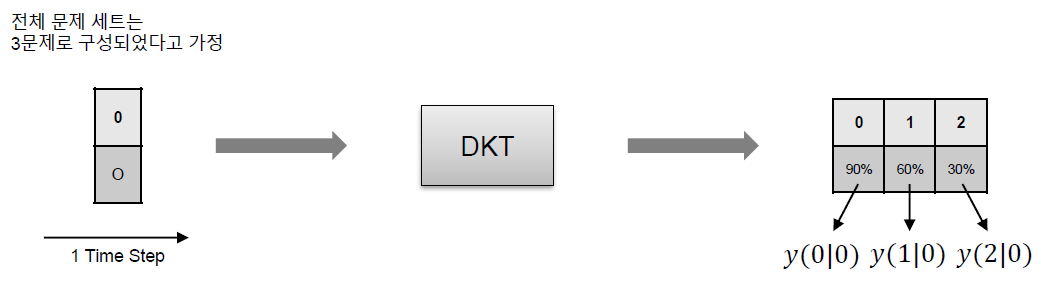
이러한 방식으로 모든 문제 쌍의 값을 정의할 수 있으며 이렇게 정의된 값들을 이용하여 모든 문제들을 Node로 하고 해당하는 \(J\) 값을 Edge로 하는 Directed Graph를 그릴 수 있게 된다.
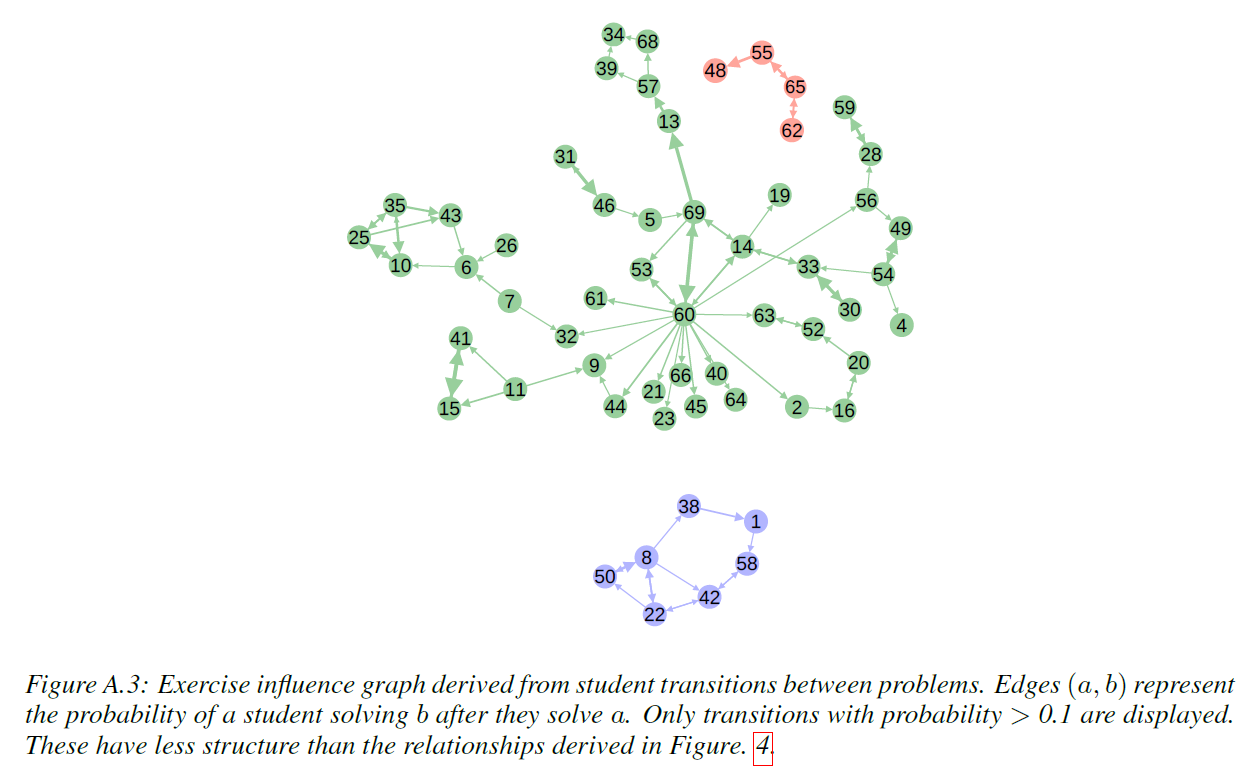(Piech, Chris, et al. “Deep knowledge tracing.” Advances in neural information processing systems. 2015.)
이렇게 만들어진 Directed Graph를 Undirected Graph로 변환하거나 또는 Graph Embedding을 통해서 새로운 Embedding Space로 Projection하는 것을 생각해 볼 수 있다. 이렇게 Embedding된 문제들은 비슷한 개념을 사용하는 문제끼리 뭉칠 것으로 기대할 수 있다.
또한 뭉쳐진 문제들 역시 뭉쳐진 문제들 사이에서 내부에 더 가까워질 수록 더 기본적인 예제 수준의 문제가 될 것이고 이를 이용하여 문제 난이도 분석 및 문제 추천, 개념 간의 거리를 이용한 커리큘럼 개선 등에 활용할 수 있을 것이라고 기대할 수 있다.
기타 참고 자료
- PyTorch로 구현한 Deep Knowledge Tracing (by Hyungcheol Noh): Knowledge Tracing Collection with PyTorch
- Dynamic Key-Value Memory Networks for Knowledge Tracing 논문 정리
수정 사항
- 2021.03.30
- 기타 참고 자료 추가
- One-Hot Encoding 부분에서 상호작용에 관한 내용 추가
- One-Hot Encoding 부분 잘못 설명되었던 부분 설명 및 그림 수정
- 전반적인 그림 잘못된 부분 수정
- 2021.04.17
- 학습 과정에서 \(\delta\)의 역할에 대한 더 자세한 설명 추가