이전 포스트에서 Markov Random Field (MRF)를 정의하기 위한 Global Markov Property에 대해서 다룬적이 있었다. 이 포스트에서 마지막에 이 성질들이 MRF의 Factorization 과정에서 중요한 정리를 유도할 때 사용된다고 언급한 바 있다. 이번 포스트에서는 이 정리를 다뤄보도록 할 생각이다.
Global Markov Property
이전에 밝힌 대로 Markov Property는 크게 3가지를 들 수 있었다. 먼저 Pairwise Markov Property는 두 개의 인접하지 않은 Random Variable 쌍은 다른 Random Variable들이 모두 관찰된 상황에서 서로 조건부 독립 관계라는 속성이다.
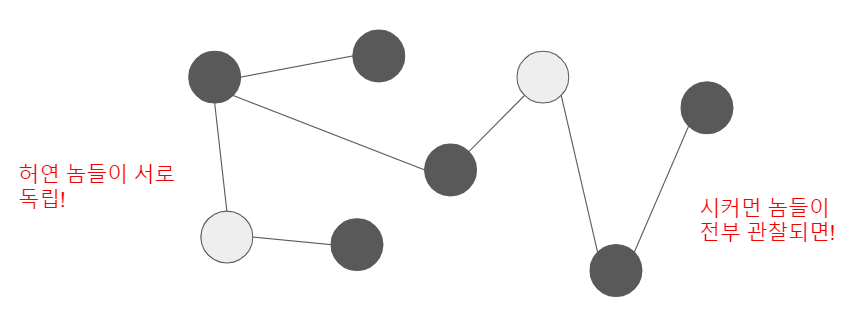
그 다음은 Local Markov Property이다. Local Markov Property는 인접한 모든 Node들, 즉 Neighborhood들이 모두 관찰된 경우 그 Node와 다른 Node들과는 전부 조건부 독립 관계라는 속성이다.
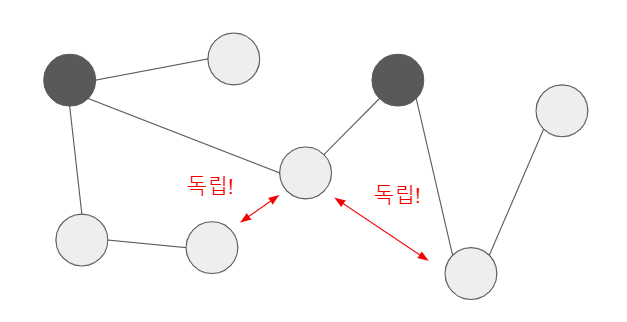
마지막으로 Global Markov Property는 어떤 주어진 Random Variable들의 집합이 어떤 다른 집합에 의해서 분리될 수 있는 경우 이 어떤 집합을 Separating Subset이라고 정의한다. 이 Separating Subset이 관찰되는 경우, 이 집합으로 인하여 분리되는 두 집합은 서로 조건부 독립 관계라는 속성이 Grobal Marko Property이다.
Hammerseley-Clifford Theorem
먼저 다음과 같은 정리가 증명되어 있다고 알려져있다:
- 어떤 Random Variable들의 집합 \(X = \{ X_1, \cdots, X_N\}\)에 대한 분포 \(P_X\)가 어떤 Factor Graph \(G\)에 대해 Factorization이 된다면, \(X\)는 \(G\)에 대한 모든 Local Markov Property들을 만족한다.
이 정리의 증명은 간단하며 여기에서 따로 소개하지는 않겠다.
그렇다면 오늘의 핵심 주제인 Hammerseley-Clifford 정리는 무엇일까? 정리의 내용은 다음과 같다:
- 어떤 Random Variable의 집합 \(X = \{ X_1, \cdots, X_N\}\)에 대한 분포 \(P_X\)가 Strictly Positive한 분포라고 가정하자. 만약 \(X\)가 어떤 Factor Graph \(G\)에 대해 Global Markov Property을 만족한다면, \(P\)는 \(G\)에 대해 Factorization이 가능하다.
이 정리의 증명은 아직 시도해보지 못하였다. 나중에라도 증명을 해본다면 소개해보도록 하겠다.
결국 이 두 정리가 하고싶은 이야기는 다음과 같다고 볼 수 있다. MRF의 정의에 따라 MRF가 갖는 성질을 바탕으로 Factorization 결과가 유일하게 결정될수도 있으며, Factorization 결과로부터 다시 MRF를 구성하는 것도 가능하다. 즉, Factorization Graph와 그 Factorization 결과는 서로 동치라는 점이다.

References
- Introduction to Statistical Relational Learning
- Information, Physics, and Computation
- Probabilistic Graphical Models