지난번에는 Random Variable들 사이의 의존성에 방향이 포함된 상황을 어떻게 형식적으로 다룰 것이냐에 대한 내용인 Bayesian Network에 대해서 다뤄보았다. 이번에는 방향이 없는 경우에는 어떻게 할 것이냐에 대한 내용을 다뤄보도록 하겠다.
Introduction to Markov Random Field
Bayesian Network가 DAG였던 것과는 다르게 Markov Random Field (MRF)는 Undirected Graphical Model 구조에 기반을 둔 모델이다. Bayesian Network와 마찬가지로 Node는 Random Variable을 나타내며 엣지는 그 Random Variable들 사이의 상호작용을 나타내게 된다. 다만 방향성이 없기 때문에 CPD로 가정할 수는 없으며 중력, 전자기력같은 영향력을 상상하면 될 것 같다.
Random Variable들 사이의 무슨 중력에 대해서 이야기하는지 도저히 이해가 안갈 수 있지만 간단한 예시를 통해서 확인해보도록 하자.
An Example of MRF: Ising Model
Ising Model은 통계 물리에서 서로 상호작용하는 원자들로 구성된 시스템의 에너지를 다루기 위해서 등장한 모델이다.
각각의 원자들은 각각 자기 자신의 Spin의 방향이 할당되어 있으며 이 값은 이진값으로 표현되게 된다. 또한 원자들은 격자 구조로 균일하게 분포되어 있다.
여기서는 원자 3개로 구성된 격자 구조를 생각해보도록 하자. 이 때 각각의 원자는 +1 또는 -1 값을 통해서 Spin 방향을 표현하게 된다. 3개의 원자들은 Spin 방향에 따라서 서로에게 영향을 주게 된다.
그렇다면 이러한 상황에서 이 시스템의 가장 안정적인 (그럴듯한, 있을법한) Spin 방향의 할당은 어떻게 될까? 아래 그림을 살펴보자.
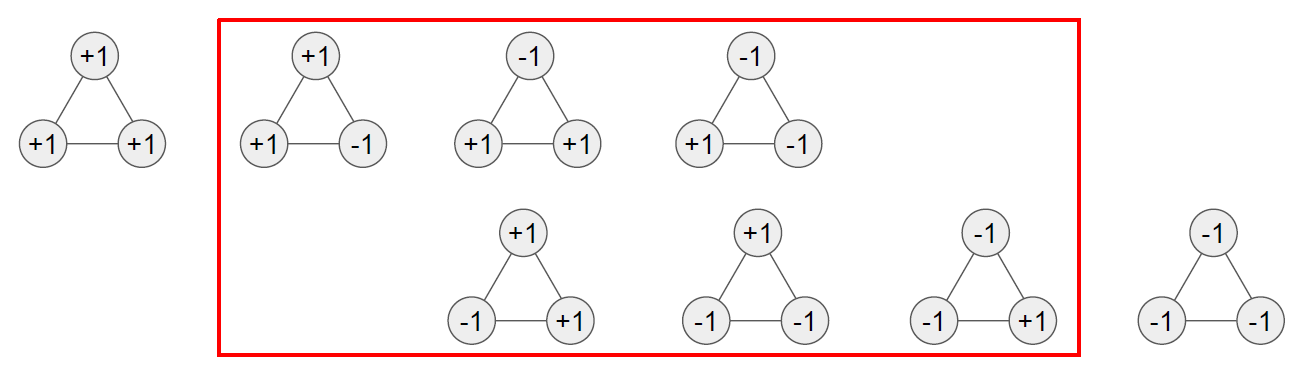
위의 그림은 가능한 Spin 방향 할당들의 Ensenble을 표현하고 있다. 위에서 붉은색으로 표시된 부분이 바로 가장 안정적인 할당들이라고 볼 수 있다.
그 이유를 설명하기 위해서는 Ising Model의 에너지 함수를 먼저 살펴봐야 할 것이다. 다음은 이징 모형의 에너지 함수이다:
\[\epsilon_{i,j}(x_i, x_j) = w_{i,j}x_i x_j.\]여기서 가중치 \(w_{i,j}\)는 대칭 함수이다:
\[w_{i,j} = w_{j, i}\]이 격자 구조에서 가중치 값들이 모두 동일하다고 가정한다면, 격자 구조 내에서의 모든 순서쌍에 대한 에너지의 총 합이 각각의 Ensemble의 상태에 대한 총 에너지 값이 될 것이다. 또한 붉은색으로 표시된 상태들이 가장 작은 에너지를 갖게 된다는 것은 간단한 계산을 통해서 확인할 수 있을 것이다.
Formal Definition of MRF
위의 Ising Model의 예시로부터 우리는 MRF의 몇 가지 특징을 확인해 볼 수 있을 것이다.
첫 번째 특징은 인접하지 않은 두 원자들의 Spin 방향은 다른 모든 원자들의 Spin 방향이 관찰된다면 서로 조건부 독립 관계를 갖는다는 점이다.
두 번째 특징은 원자 각각의 Spin 방향은 자기 주위에 인접한 원자들의 Spin 방향이 관찰된다면 그 외의 원자들의 Spin 방향들과 모두 조건부 독립 관계를 갖는다는 점이다.
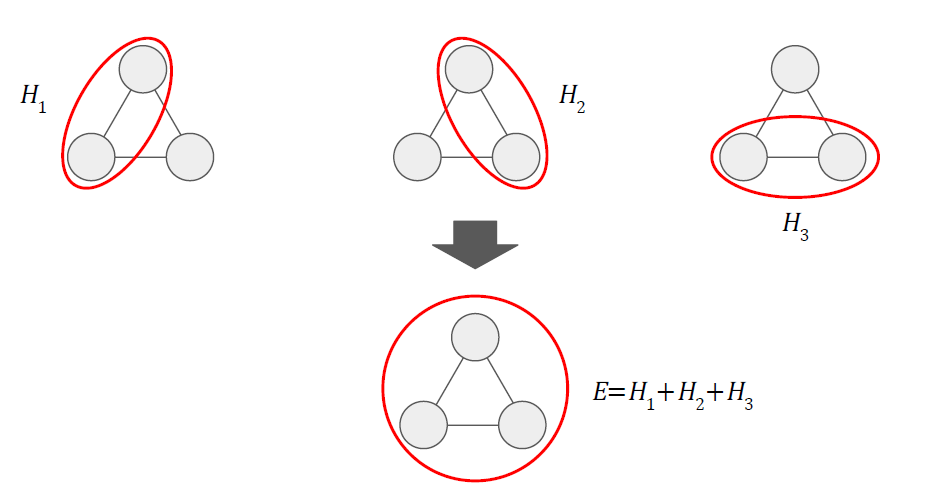
세 번째 특징은 원자 묶음 2개에 대해서 그 묶음 2개를 완벽하게 분리하는 새로운 묶음의 원자들의 Spin 방향이 관찰된다면 각각의 원자 묶음 2개의 Spin 방향은 서로들간의 Spin 방향들과 조건부 독립 관계를 갖는다는 점이다.
첫 번째 특징은 Pairwise Markov Property라고 한다. 두 번째 특징은 Local Markov Property라고 한다. Local Markov Property는 이전 포스트인 Bayesian Network에 대한 포스트에서 등장했던 것을 기억할 것이다. 세 번째 특징은 Global Markov Property이다.
일반적으로 Global Markov Property를 만족한다면 이전 두 가지 Markov Property들도 함께 만족한다고 알려져 있다. 만족하지 않는 경우도 있으나 일반적이지 않은 상황이며 여기서 다룰 내용은 아니라고 생각되어 다루지 않도록 하겠다.
어쨌든 Global Markov Property를 이용하여 MRF를 다시 정의하면 다음과 같다:
- \(G=(V, E)\)를 Undirected Graph라고 하자. 만약 주어진 Random Variable 집합 \(\{ X_i\}_{i\in V}\)이 아래의 조건이 만족한다면 이 Random Variable들은 그래프 \(G\)에 대해서 MRF를 형성한다:
- 주어진 Random Variable들의 집합의 부분집합 \(X_A, X_B, X_S\)에 대해서 \(X_S\)가 나머지 두 부분집합을 연결하는 모든 경로를 다 지나가는 상황에서 다음의 조건을 만족:
이러한 Global Markov Property는 앞으로 MRF의 Factorization 과정에서 중요한 정리를 유도할때 사용되게 된다.
References
- Introduction to Statistical Relational Learning
- Information, Physics, and Computation
- Probabilistic Graphical Models