#probability #statistics #machine learning #deep learning #natural language processing

이번 포스트에서는 인공 신경망 기반 자연어 처리 방법론에서 기본적으로 활용되는 단어 임베딩 방법론인 Word2Vec, 특히 이를 훈련하기 위한 대표적인 모델인 Skip-Gram모델을 중심으로 정리해보도록 한다. 또한 Skip-Gram 모델 뿐 아니라 이를 잘 훈련시키기 위한 다양한 방법론들 역시 다뤄본다.

목차

단어 임베딩

이전 포스트에서 간단히 설명하였듯 인공 신경망 기반의 자연어 처리 방법론들은 기본적으로 토큰(단어)에 대한 벡터화된 표현(Representation) 방식을 따른다. 이를 단어 임베딩(Word Embedding)이라고 부르며 우리가 원하는 특징을 지닌 벡터 공간으로 토큰을 투영하여 표현하게 된다. 단어 임베딩이라고 부르는 이유는 영어 문장의 토큰화는 단어(Word) 단위로 수행이 되며 이 단어 토큰에 대한 표현을 구해낸다는 의미로 단어 임베딩이라고 부르게 된다.

우리가 원하는 벡터 공간의 특징은 기본적으로 Distributional Hypothesis라는 대전제를 따르게 된다. 이는 말뭉치 내에서 가깝게 등장하는 단어들은 그 의미상으로도 유사할 것이라는 가정이다. 실제로 Word2Vec에서는 이 가정을 통해서 훈련을 수행하였고 결과물도 꽤 의미가 있어 보인다.

Skip-Gram 모델

Skip-Gram 모델은 기본적으로 좋은 단어 표현을 위한 모델이며 주어진 단어를 바탕으로 주위에 있는 단어들이 무엇일지를 예측할 수 있는 모델이다. 이는 지극히 자연스럽게 Distributional Hypothesis를 따른다.

좀 더 형식적으로는, 주어진 단어들의 나열 \(w_1, w_2, \cdots, w_T\)에 대하여 Skip-Gram 모델의 목적 함수(Objective Function)은 다음과 같은 로그 확률의 평균으로 정의한다:

\[\frac{1}{T} \sum_{t=1}^T \sum_{-c \leq j \leq c, j \neq 0} \log p(w_{t+j} \vert w_t).\]

여기서 \(c\)는 훈련용 문맥(Training Context)의 크기이며 이 훈련용 문맥은 중간 단어 \(w_t\)에 대한 함수이다. 더 큰 크기의 훈련용 문맥을 통해 훈련한다면 더 높은 정확도를 기대할 수 있겠지만 그 만큼 훈련 시간이 오래 걸릴 것이다. Skip-Gram 모델을 통해서 다루는 \(p(w_{t+j} \vert w_t)\)는 기본적으로 다음의 형태를 지닌다:

\[p(w_O \vert w_I) = \frac{\exp \left( \mathbf{u}_{w_O}^\text{T} \mathbf{v}_{w_I} \right)}{\sum_{w=1}^W \exp \left( \mathbf{u}_w^\text{T} \mathbf{v}_{w_I} \right)}.\]

이는 Softmax 함수를 활용하는 간단한 접근이다. 또한 여기서 \(\mathbf{v}_w\)와 \(\mathbf{u}_w\)은 각각 단어 \(w\)에 대한 입력/출력 벡터 표현이고, \(W\)는 단어 사전의 총 단어 개수이다. 여기서 입력/출력 벡터 표현이 서로 다른 이유는 모든 단어들은 자신이 입력 단어 위치에 있는 경우와 출력 단어 위치에 있는 경우에 그 역할이 달라야 한다는 가정이 담겨 있다. 벡터 표현이 전혀 다름으로써 그 역할의 다름을 반영할 수 있는 것이다.

Softmax 함수를 활용한 이러한 방식의 확률 계산법은 사실 굉장히 큰 문제가 있다. 바로 이 계산의 계산 복잡도가 단어 사전의 크기인 \(W\)만큼 크기 때문이다. 그 이유는 Softmax 함수의 분모 때문이다. 전체 단어 사전을 순회하면서 모든 값들을 더해줘야 하는 계산 방식이 바로 그 문제의 핵심이다. 일반적을 단어 사전의 크기는 작게는 \(10^5\)에서 크게는 \(10^7\)에 이를 정도로 매우 크다. 이는 엄청난 부하를 일으키게 될 것이다.

이러한 계산 복잡도 문제를 해결하기 위한 방향으로 일반적으로는 크게 2가지 방법론이 존재한다. 첫 번째는 Hierarchical Softmax라는 방법이고, 두 번째는 Negative Sampling이라는 방법이다.

Hierarchical Softmax

Hierarchical Softmax는 계산 복잡도 \(W\)인 Softmax의 연산을 \(\log_2 W\)로 줄일 수 있는 방법이다. 즉 \(W\)개의 전체 단어를 탐색하는 것이 아닌 \(\log_2 W\)개의 단어만을 탐색하는 방식이라는 것이다. 이를 위해서는 기본적으로 단어 사전에 속한 단어들을 노드로 하는 이진 트리 구조의 표현을 구축해야 한다.

이진 트리

이진 트리(Binary Tree)는 트리(Tree) 형태의 자료 구조의 한 종류이다. 기본적으로 트리는 노드(Node)와 방향이 있는 에지(Edge)로 이루어진 유향 그래프 (Directed Graph) 형태의 자료 구조의 한 종류이며 하나의 노드에서 출발하여 다른 노드들을 순회하여 자기 자신에게 되돌아오는 순환 연결이 없는 그래프이다. 이러한 형태의 그래프를 유향 비순환 그래프(Directed Acyclic Graph, DAG)라고도 한다. 트리는 이러한 DAG 중 모든 노드에 대한 부모 노드가 항상 한 개 이하인 경우를 말한다. 트리는 계층화된 노드들을 표현하는데 적절한 형태의 자료 구조이다.

이진 트리는 이러한 트리들 중 모든 노드들에 대하여 항상 자식이 2개 이하인 트리를 이진 트리라고 한다. 이진 트리는 인덱싱이 되어있는 자료들에 대해서 탐색 알고리즘에 아주 효율적인 구조인데 모든 노드들을 탐색하며 원하는 노드를 찾는 방식이 아닌 트리의 깊이만큼만 검색을 하면 되기 때문이다.

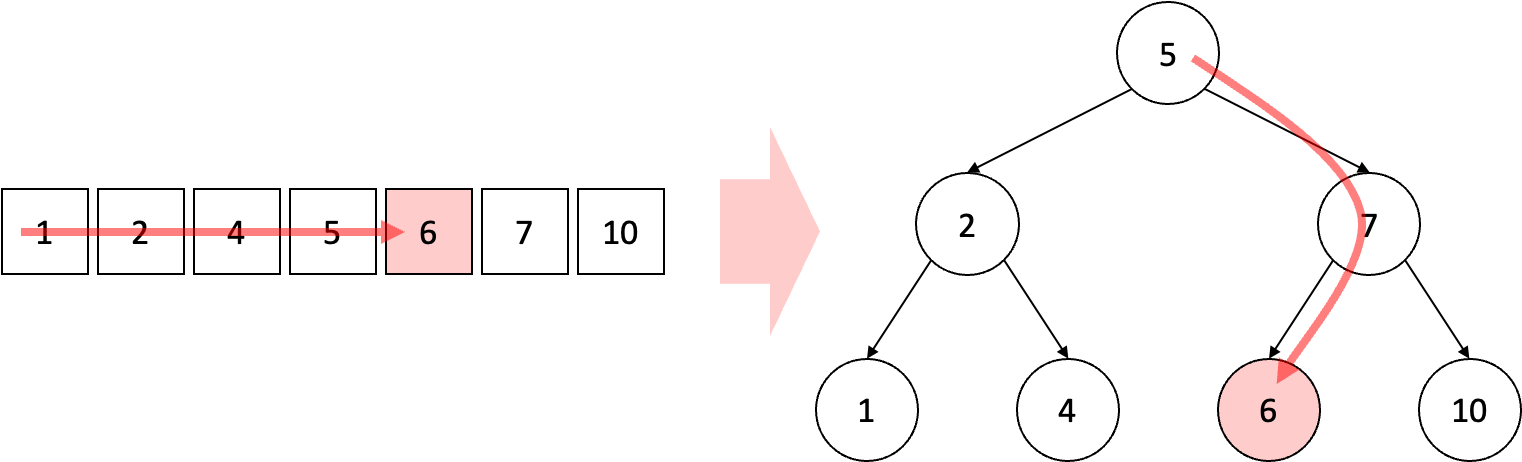
위 그림은 배열 [1, 2, 4, 5, 6, 7, 10]에서 6을 탐색하는 과정을 일반 배열에서와 배열을 적절한 이진 트리로 구성하여 진행하는 과정을 나타내고 있다. 일반 배열에서는 결국 요소 하나하나를 살펴보면서 내가 찾고자 하는 값인 6과 일치하는지 여부를 확인하여 탐색을 진행하게 된다. 이는 최악의 경우에 모든 요소를 다 살펴보는 결과로 이끌게 되며 이는 계산 복잡도가 \(O(n)\)으로 표현될 수 있다. 여기서 \(n\)은 찾고자 하는 대상이 되는 자료 구조의 크기이며 위의 예시의 경우 배열의 크기인 7이 될 것이다.

반면 이진 트리의 경우를 살펴보자. 먼저 루트(Root) 노드인 5와 찾고자 하는 노드인 6의 크기를 비교한다. 여기서 6이 5보다 크기 때문에 오른쪽에 있는 자식 노드의 방향으로 탐색을 재개한다. 그 다음으로 다시 현재의 노드인 7과 비교하며 6은 7보다 더 작기 때문에 왼쪽 자식 노드인 6을 찾아낼 수 있다. 이 경우 일반 배열에서처럼 6번 탐색을 한 것이 아니라 총 3번 탐색을 하였으며, 최악의 경우에도 트리의 최대 깊이를 넘지 않고 탐색이 가능하다.

그러면 이진 트리의 최대 깊이는 어떻게 구할 수 있을까? 계산 복잡도를 논하기 위해서 이진 트리의 최대 깊이가 가장 큰 상황을 고려해야 할 것이다. 이를 모든 부모 노드들에 대해서 자식 노드의 개수가 2인 정 이진 트리(Full Binary Tree)의 형태로부터 확인할 수 있다.

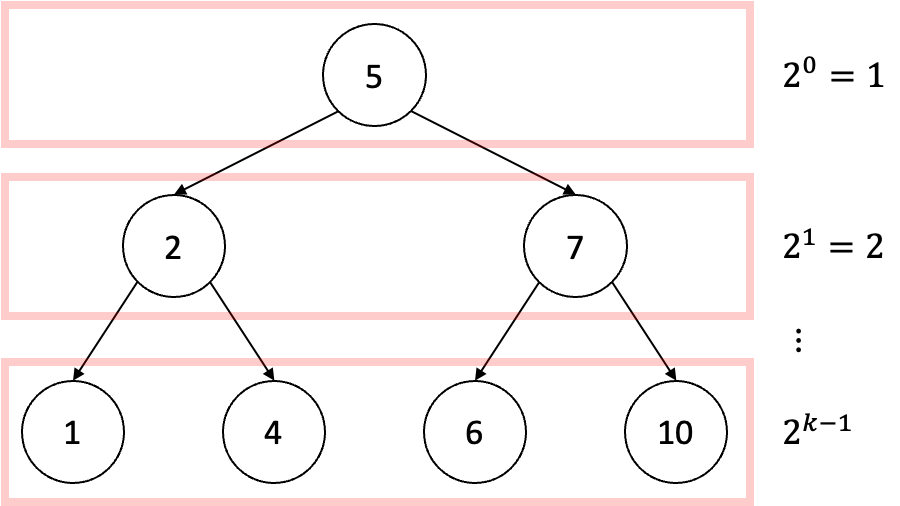
위의 그림은 최대 깊이가 \(k\)인 정 이진 트리의 전체 노드 개수를 구하는 과정을 설명하기 위한 그림이다. 단계를 하나씩 내려가며 확인할 수 있는 단계별 노드의 개수는 현재 단계 \(l\)에 대해서 \(2^{l - 1}\)개인 것을 확인할 수 있다. 즉 최대 깊이가 \(k\)인 정 이진 트리의 전체 노드 개수는 다음과 같다:

\[\sum_{l=1}^k 2^{l - 1} = 2^k - 1.\]

만약 전체 노드의 개수가 \(n\)이라면 이 이진 트리가 가질 수 있는 최대 깊이는 역으로 다음과 같이 구할 수 있다:

\[n = 2^k - 1. \ \ \ \ \Longrightarrow \ \ \ \ k = \log_2(n + 1) = O\left( \log_2(n) \right).\]

즉, 최악의 경우에도 이진 트리를 활용하면 계산 복잡도는 \(O\left( \log_2(n) \right)\)이 된다. 이는 계산 복잡도가 \(O(n)\)인 일반 배열보다 훨씬 계산 복잡도가 낮다.

허프만 코딩

허프만 코딩(Huffman Coding)은 원래 정보 이론 분야에서 데이터를 구성하는 각각의 심벌의 등장 빈도를 통해서 이 데이터를 압축하는 방법론 중 하나이다. 허프만 코딩에서는 먼저 빈도수를 활용하여 각 심벌들을 리프(Leaf) 노드로 하는 이진 트리를 구축하는데 Hierarchical Softmax에서는 이 방법을 이용하여 단어 사전의 이진 트리 구축을 수행한다.

그러면 단어 사전의 이진 트리를 어떻게 구축하는지 알아보자. 기본적으로 허프만 코딩을 통해서 생성되는 이진 트리는 빈도수를 기준으로 빈도수가 낮은 노드의 깊이를 더 깊게 가져가려고 한다. 그 이유는 빈도수가 높은 노드의 탐색의 깊이를 낮게하고 빈도수가 낮은 노드의 탐색의 깊이를 깊게 함으로써 평균적인 탐색 횟수를 줄이고자 하기 때문이다. 이를 위해서는 먼저 주어진 말뭉치로부터 단어 사전과 그 단어 각각의 빈도수를 추출한 이후에 구축을 시작해야 한다. 여기서는 예시를 위해서 단어 사전이 A, B, C, D, E, F라는 단어로 구성되어 있고 이들 빈도수가 각각 2, 3, 5, 7, 9, 13이라고 가정하자. 가장 먼저 할 작업은 빈도수를 기준으로 이 단어들을 정렬하는 것이다.

정렬된 단어들 중에서 가장 빈도수가 낮은 단어부터 두 단어씩 묶어서 트리를 형성하기 시작한다. 현재 예시에서는 단어 A, B를 먼저 묶어야 할 것이다. 두 단어를 묶고 나서 두 단어의 부모 노드를 만들고 이 부모 노드의 빈도수는 단어 A, B의 합인 5로 설정한다.

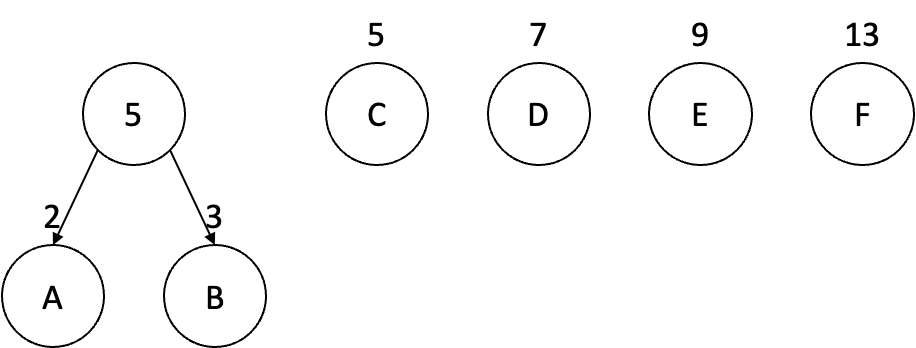
이제 여기부터 그 다음 빈도수의 단어와 비교를 한다. 현재 노드의 빈도수 5와 단어 C의 빈도수를 비교하여 단어 C의 빈도수가 5보다 더 높거나 같으면 현재 노드와 단어 C를 또 묶어서 새로운 부모 노드 휘하로 구성한다.

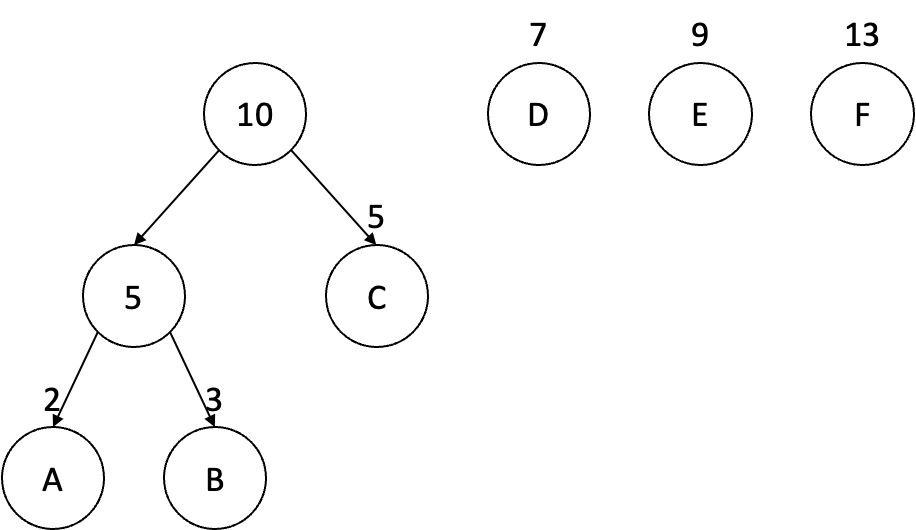
이제 빈도수 총합 10인 부모 노드와 그 다음 단어 D의 빈도수를 또 비교한다. 만약 단어 D의 빈도수가 10보다 작다면 그 다음 단어인 E의 빈도수와 더하여 그 값을 10과 비교해본다. 여기서는 16이 될 것이고 이는 10보다는 높기 때문에 16 빈도수의 새로운 부모 노드를 형성하는 이진 서브 트리를 구성하여 오른쪽으로 정렬한다.

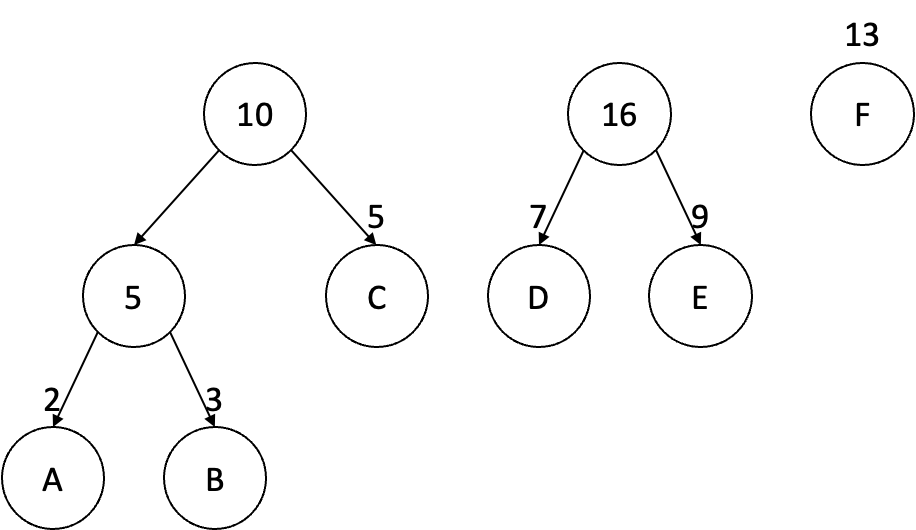
이제 마지막으로 남은 단어 F는 빈도수를 두 부모 노드의 빈도수인 10, 16과 비교하여 적절한 위치에 두고 이진 서브 트리를 구성한다.

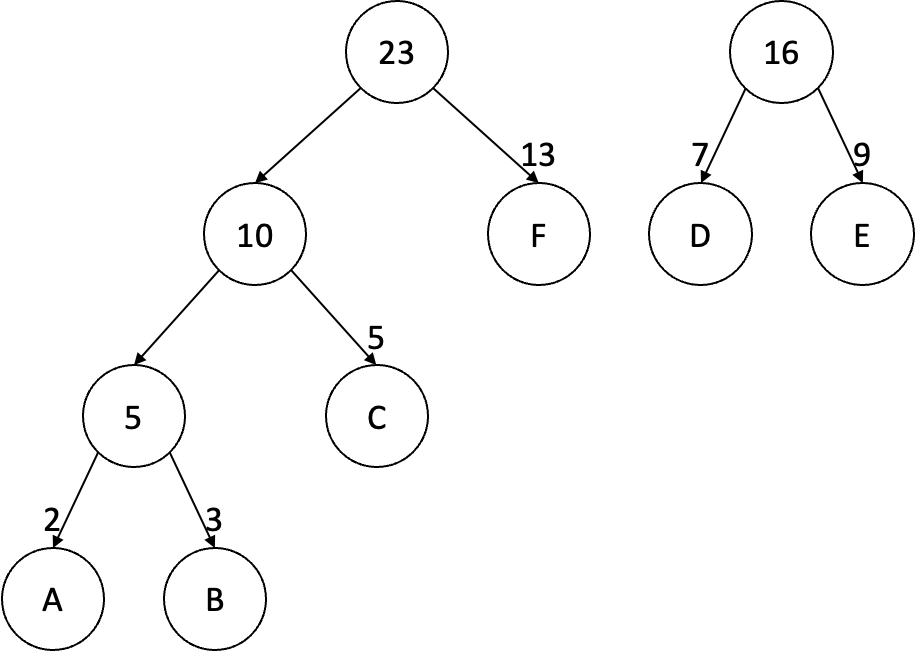
최종적으로 형성된 이진 트리는 다음과 같다.

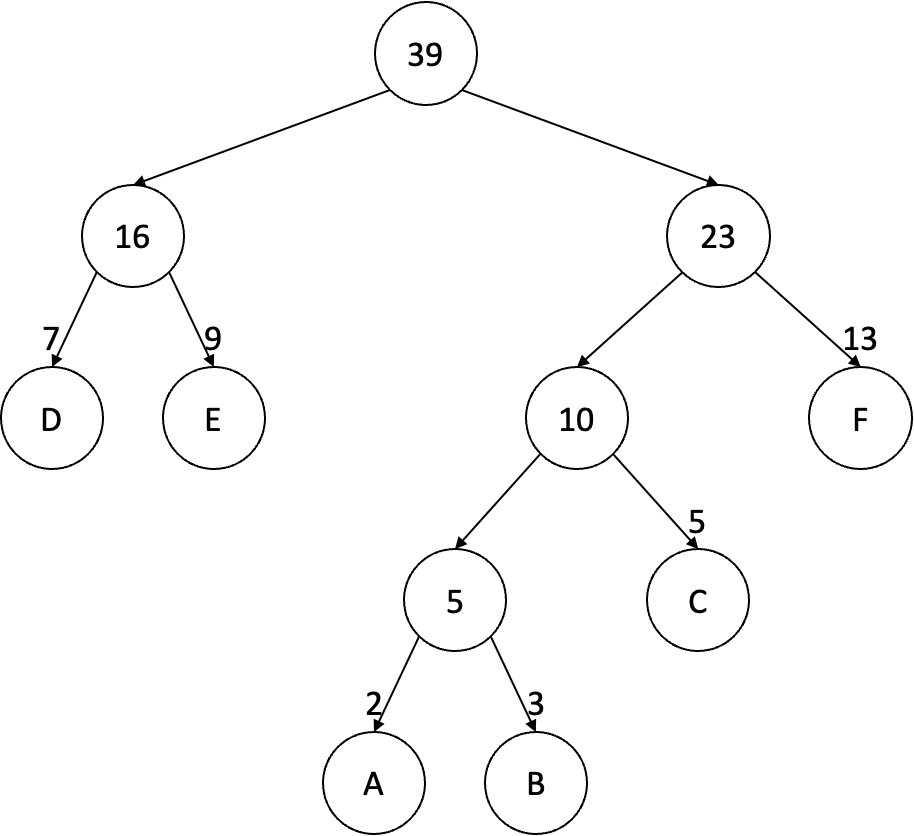
Hierarchical Softmax

이제 본격적으로 Hierarchical Softmax에 대해서 다뤄보자. Hierarchical Softmax의 기본적인 원리는 단어 각각에 대해서 자신의 임베딩 벡터와 비교하고자 하는 다른 단어의 임베딩 벡터 사이의 유사도를 측정하는 대신, 이진 트리 상에서 비교하고자 하는 다른 단어로의 경로상의 노드들의 임베딩 벡터와의 유사도를 측정하는 방식으로 유사도 계산량을 줄이겠다는 것이다.

설명만 들으면 복잡하기 때문에 예시를 활용해보도록 하자. 위에서 허프만 코딩을 설명하기 위해서 사용했던 단어 A, B, C, D, E, F에 대한 이진 트리를 바탕으로 설명을 진행해보자. 우리는 이를 위해서 \(p(\text{C} \vert \text{E})\)를 구하는 과정을 따라가 볼 것이다. 즉, 입력 단어는 E이고 출력 단어는 C인 경우이다.

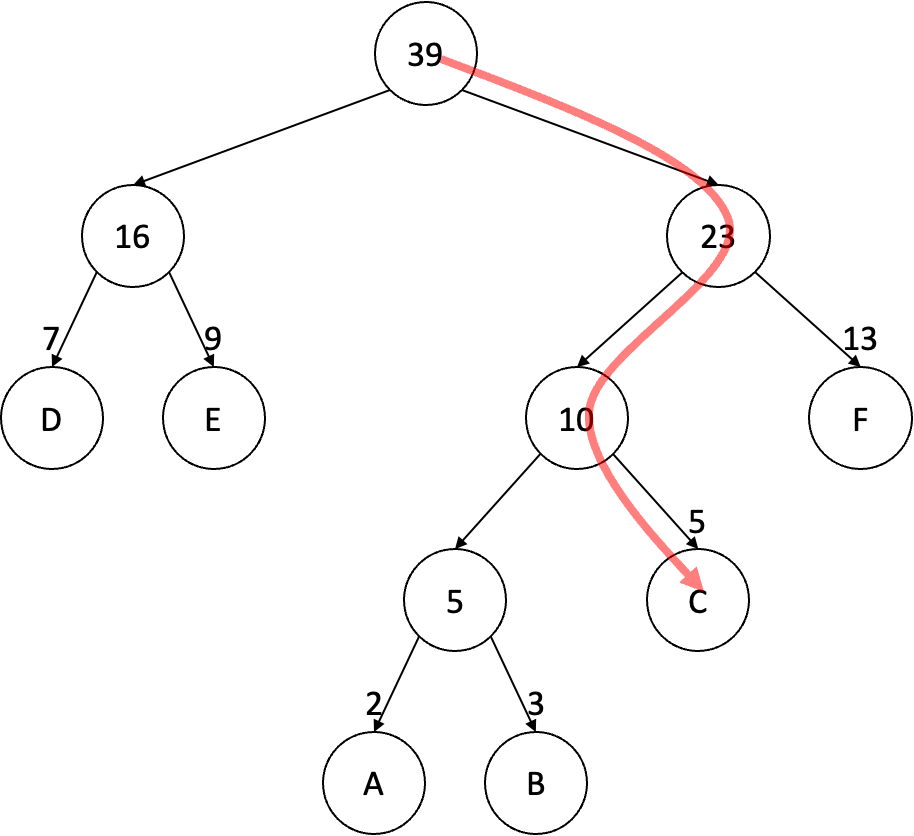
일단 가장 상단에 있는 루트 노드와 임베딩 벡터 사이의 유사도를 먼저 측정한다. 유사도 측정에 있어서 가장 주의해야 할 사항은 다음과 같다. 일단 현재 경로상의 자식 노드가 현재 노드의 왼쪽 노드인지 여부를 확인해야 한다. 물론 이 과정은 특정 방향으로 고정만하면 되기 때문에 오른쪽이어도 상관은 없다. 다만 이 반복되는 과정 속에서 항상 한쪽 방향인지의 여부를 확인해야 한다. 어쨌든 경로가 왼쪽으로 이어지는지 여부에 따라서 유사도 계산은 달라진다. 현재 루트 노드의 경우 경로는 오른쪽으로 빠지게 된다. 이 경우 루트 노드의 임베딩 벡터를 \(\mathbf{u}_{39}\)라고 한다면 유사도 계산은 다음과 같다:

\[\sigma \left( -\mathbf{u}_{39}^\text{T} \mathbf{v}_\text{E} \right).\]

여기서 \(\sigma\)는 로지스틱 함수(Logistic Function) 또는 시그모이드 함수(Sigmoid Function)라고 불리우는 함수이다. 그 다음으로 단어 C로의 경로를 따라가며 만나는 다음 노드인 23 노드와 유사도를 계산한다. 여기서 23 노드는 경로상 자식 노드가 왼쪽으로 이어지기 때문에 다음과 같이 계산한다:

\[\sigma \left( \mathbf{u}_{23}^\text{T} \mathbf{v}_\text{E} \right).\]

그리고 단어 C로의 경로상에서 만날 수 있는 그 다음 노드인 10 노드와 유사도를 계산한다. 여기서는 오른쪽으로 이어지기 때문에 다음과 같이 계산하면 된다:

\[\sigma \left( -\mathbf{u}_{\text{10}}^\text{T} \mathbf{v}_\text{E} \right).\]

이렇게 구한 유사도들을 바탕으로 최종적으로 우리가 구하고자 했던 \(p(\text{C} \vert \text{E})\)는 다음과 같이 계산한다:

\[p(\text{C} \vert \text{E}) = \sigma \left( -\mathbf{u}_{39}^\text{T} \mathbf{v}_\text{E} \right) \cdot \sigma \left( \mathbf{u}_{23}^\text{T} \mathbf{v}_\text{E} \right) \cdot \sigma \left( -\mathbf{u}_{10}^\text{T} \mathbf{v}_\text{E} \right).\]

이 과정을 일반적으로 기술하면 다음과 같이 쓸 수 있다:

\[p(w \vert w_I) = \prod_{j = 1}^{L(w) - 1} \sigma \left( \left[ \left[ n(w, j + 1) = \text{ch}(n(w, j)) \right] \right] \cdot \mathbf{u}_{n(w, j)}^\text{T} \mathbf{v}_{w_I} \right).\]

여기서 \(n(w, j)\)는 루트부터 단어 \(w\)까지의 경로상에서 \(j\)번째 노드를 의미하고, \(L(w)\)는 이 경로의 길이이다. 즉 \(n(w, 1)\)은 루트 노드이고 \(n(w, L(w))\)는 \(w\)가 될 것이다. 또한 모든 경로상의 노드 \(n\)에 대하여 \(\text{ch}(n)\)은 노드 \(n\)의 어떤 임의의 고정된 방향의 자식 노드를 의미하는데 여기서는 왼쪽 자식 노드로 고정하기로 한다. 그리고 \([[x]]\)는 \(x\)가 참이면 1, 거짓이면 -1을 반환하는 지시 함수이다(Indicator Function). 결과적으로 이런 방식으로 계산을 한다면 \(p(w_O \vert w_I)\)를 계산하기 위해서 필요한 비용은 \(L(w_O)\)일 것이고 이는 절대 \(\log_2(W)\)를 넘지 않게 된다.

이제 이 Hierarchical Softmax를 위의 예시를 바탕으로 해석을 해보도록 하자. 기본적으로 Hierarchical Softmax의 아이디어는 결합 확률을 조건부 확률로 분해(Factorization)하는 아이디어를 기반으로 한다. 즉, 단어들의 클래스(Class)를 분류하고 이 클래스를 통해서 조건부 확률로 기술하는 것에서부터 시작한다. 예시를 위해서 우리가 구하고자 하는 분포를 \(p(Y \vert X)\)라고 해보자. 그러면 \(p(Y \vert X)\)는 \(Y\)가 속한 클래스 \(C\)에 대하여 다음과 같이 분해될 수 있다:

\[p(Y \vert X) = p(Y \vert C, X) \cdot p(C \vert X).\]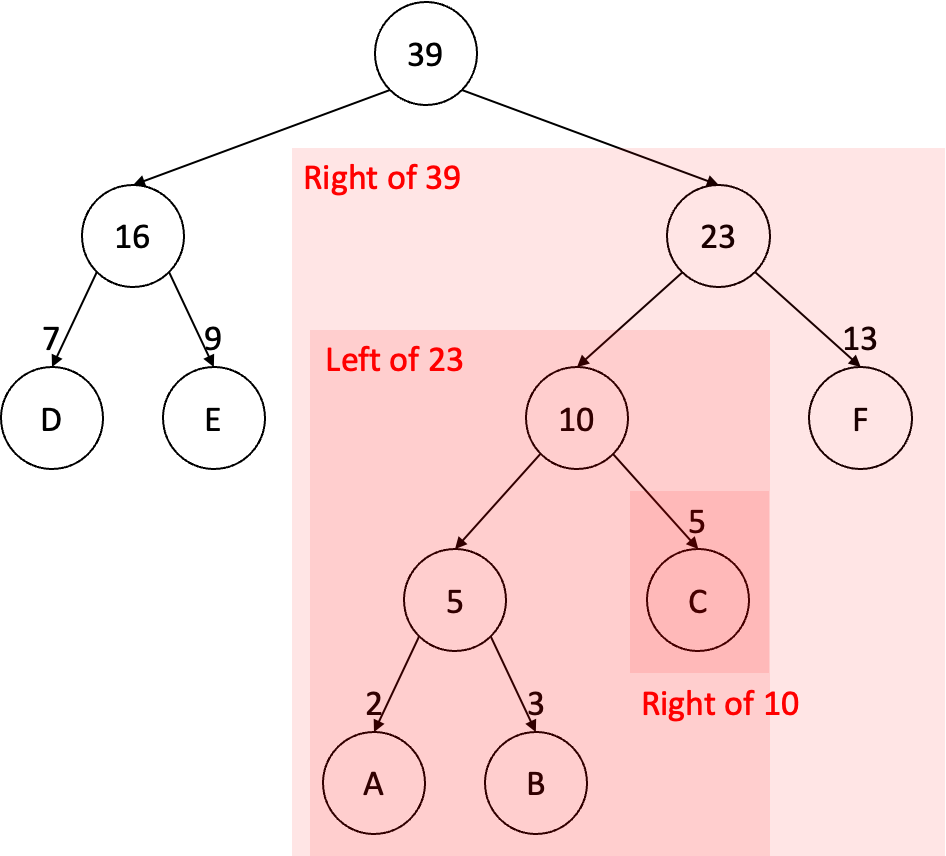

우리는 이진 트리를 통해서 주어진 단어들 각각이 어떤 클래스에 속하는지를 구분하여 기술할 수 있다. 위의 예시에서 단어 C는 39 노드의 오른쪽 클래스, 23 노드의 왼쪽 클래스, 10 노드의 오른쪽 클래스에 속한다는 것을 확인할 수 있다. 이를 통해서 \(p(C \vert E)\)는 다음과 같이 분해될 수 있다:

\[\begin{array}{rl} p(C \vert E) = & p(\text{Right of 39} \vert E) \\ & \cdot p(\text{Left of 23} \vert \text{Right of 39}, E) \\ & \cdot p(\text{Right of 10} \vert \text{Left of 23}, \text{Right of 39}, E) \\ & \cdot p(C \vert \text{Right of 10}, \text{Left of 23}, \text{Right of 39}, E). \end{array}\]

여기서:

\[p(C \vert \text{Right of 10}, \text{Left of 23}, \text{Right of 39}, E) = p(C \vert \text{Right of 10}) = 1\]

이므로 최종적인 분해 결과는 다음과 같다:

\[\begin{array}{rl} p(C \vert E) = & p(\text{Right of 39} \vert E) \\ & \cdot p(\text{Left of 23} \vert \text{Right of 39}, E) \\ & \cdot p(\text{Right of 10} \vert \text{Left of 23}, \text{Right of 39}, E). \end{array}\]

여기서 Hierarchical Softmax는 다음과 같은 모델링을 수행하게 된다:

\[\begin{array}{l} p(\text{Right of 39} \vert E) = \sigma \left( -\mathbf{u}_{39}^\text{T} \mathbf{v}_\text{E} \right), \\ p(\text{Left of 23} \vert \text{Right of 39}, E) = \sigma \left( \mathbf{u}_{23}^\text{T} \mathbf{v}_\text{E} \right), \\ p(\text{Right of 10} \vert \text{Left of 23}, \text{Right of 39}, E) = \sigma \left( -\mathbf{u}_{10}^\text{T} \mathbf{v}_\text{E} \right). \end{array}\]

Negative Sampling

Negative Sampling은 Hierarchical Softmax의 좋은 대체제 중 하나이다. Hierarchical Softmax는 위에서 다뤘듯이 전체 단어 사전을 다 순회하며 유사도를 측정하고 이를 Softmax의 정규화하는데 사용하는 대신 필요한 몇 가지 벡터들과의 유사도만을 측정하여 정규화하는 방식으로 대체하는 방법론이었다. Negative Sampling도 마찬가지로 전체 유사도를 다 측정하는 방법이 아닌 특정 몇가지의 유사도 측정만을 가지고 Softmax 정규화를 수행한다.

그러면 Negative Sampling에서는 이를 어떻게 수행하는지 살펴보자. 일단 이름에서 알 수 있듯 Nagative Sampling은 Negative Sample을 추출하고 이에 대한 정규화를 수행하는 것이다. 이를 위해서 Log Softmax를 살펴보자:

\[\log p(w_O \vert w_I) = \mathbf{u}_{w_O}^\text{T} \mathbf{v}_{w_I} -\log \sum_{w=1}^W \exp \left( \mathbf{u}_w^\text{T} \mathbf{v}_{w_I} \right).\]

Skip-Gram 모델에서는 이를 목적 함수로 두고 최대화하는 최적화 문제를 풀게 된다. 즉 현재 주어진 입력 단어 \(w_I\)와 출력 단어 \(w_O\)의 임베딩 벡터 사이의 유사도는 가능한 증가시키려고 하면서 입력 단어 \(w_I\)의 임베딩 벡터와 (사실은 \(w_I\)와 \(w_O\)를 모두 포함하기는 하지만) \(w_O\)가 아닌 단어들의 임베딩 벡터 사이의 유사도는 가능한 감소시키려고 할 것이다.

즉, 여기서 \(w_O\)는 Positive Sample, 그 외의 단어들은 Nagative Sample이라고 해석할 수 있다. Nagative Sampling 방법은 이러한 가능한 모든 Nagative Sample을 모두 순회하는 것이 아닌 특정 몇 개의 Nagative Sample만을 추출하여 활용하는 방법론이다.

이를 수행하는 Nagative Sampling의 목적 함수는 다음과 같이 기술할 수 있다:

\[\log p(w_O \vert w_I) = \log \sigma \left(\mathbf{u}_{w_O}^\text{T} \mathbf{v}_{w_I} \right) + \sum_{i = 1}^k \mathbb{E}_{w_i \sim p_n(w)} \left[ \log \sigma \left( -\mathbf{u}_{w_i}^\text{T} \mathbf{v}_{w_I} \right) \right].\]

이 목적 함수는 Skip-Gram의 목적 함수에서 모든 \(\log p(w_O \vert w_I)\)를 대체하게 된다. 즉, Nagative Sampling은 어떤 특정 잡음 분포(Noise Distribution) \(p_n(w)\)로 부터 추출된 \(k\)개의 Nagative Sample만을 가지고 목적 함수를 계산하게 된다. 이는 Hierarchical Softmax의 경우와 마찬가지로 전체 단어 사전을 순회하지 않고 \(k\)개의 단어만을 순회하기 때문에 훨씬 계산 비용을 절감할 수 있다.

그렇다면 잡음 분포의 선택은 어떻게 해야 할까? 일단 기본적으로 Nagative Sampling에서의 잡음 분포의 선택은 자유로운 파라미터로써 설정되어있긴 하다. 일반적으로 가장 성능이 좋다고 알려진 분포는 유니그램(Unigram) 분포 \(U(w)\)를 적당히 조작한 다음의 분포이다:

\[p_n(w) = \frac{U(w)^{3/4}}{Z}.\]

유니그램은 주어진 단어에 대해서 분포가 빈도수에 정확히 비례한다. 따라서 빈도수에 \(3/4\)승 만큼의 조작을 해준 수치에 비례하는 분포가 실험적으로 가장 좋은 성능으로 알려져있는 것이다.

Subsampling of Frequent Words

영어를 기준으로 매우 거대한 말뭉치에서 가장 많이 등장하는 단어들은 “in”, “the”, “a”와 같은 단어들이다. 이러한 단어들은 일반적인 다른 단어들에 비해서 포함하고 있는 정보량이 매우 낮다. (사실 정보 이론적인 관점으로는 더 적게 등장하는 심벌일수록 정보량이 높다고 정의하기는 한다.) 예를 들면 Skip-Gram 모델은 “France”와 “the”라는 두 단어가 동시에 관찰되는 것보다 “France”와 “Paris”라는 두 단어가 동시에 관찰되는 것으로부터 더 많은 정보를 얻을 것이다. 왜냐하면 “the”는 거의 모든 단어들과 함께 등장하기 때문이다. 또한 이는 반대로 자주 등장하는 단어들의 벡터 표현은 Skip-Gram 모델 훈련을 진행하며 크게 변화하지는 않을 것이라는 점도 유추해볼 수 있다.

이러한 데이터 불균형 문제를 해소하기 위하여 나온 방법이 바로 Subsampling of Frequent Words이다. 이 방법의 골자는 훈련용 데이터에서 등장하는 각 단어 \(w\)가 특정 확률로 훈련 과정에서 배제되는 것이다. 이 확률은 다음과 같은 형태를 가진다:

\[p(w) = 1 - \sqrt{\frac{t}{f(w)}}.\]

여기서 \(f(w)\)는 단어 \(w\)의 빈도수이고 \(t\)는 특정 문턱(Threshold) 값이다. 문턱 값은 보통 \(10^{-5}\)를 준다고 한다. 이러한 Subsampling 형식은 빈도수가 \(t\)를 넘는 단어는 매우 공격적으로 배제하고 그렇지 않은 경우는 그 정도에 따라 보존한다는 의미를 담고 있다.

Word2Vec 훈련 결과 분석

Word2Vec 모델이 잘 훈련이 되었는지 확인하기 위해서 많이 활용하는 태스크는 Word Analogy 테스트이다. 이 태스크는 크게 두 분류로 나눠지는데 하나는 문법적인 요소를 다루는 Syntactic Analogy이고 나머지 하나는 의미론적인 요소를 다루는 Semantic Analogy이다. Syntactic Analogy의 예시는 “Quick”과 “Quickly”의 관계와 “Slow”와 “Slowly”의 관계가 얼마나 비슷한지를 확인하는 것을 들 수 있다. 반면 Semantic Analogy의 예시는 “Germany”와 “Berlin”의 관계와 “France”와 “Paris”의 관계가 얼마나 비슷한지를 확인하는 것을 들 수 있겠다. 이에 대한 테스트는 “Quickly”의 벡터, “Quick”의 벡터의 차이 벡터와 “Slowly”의 벡터, “Slow”의 벡터의 차이 벡터가 얼마나 유사한지를 확인하는 방법으로 진행된다.

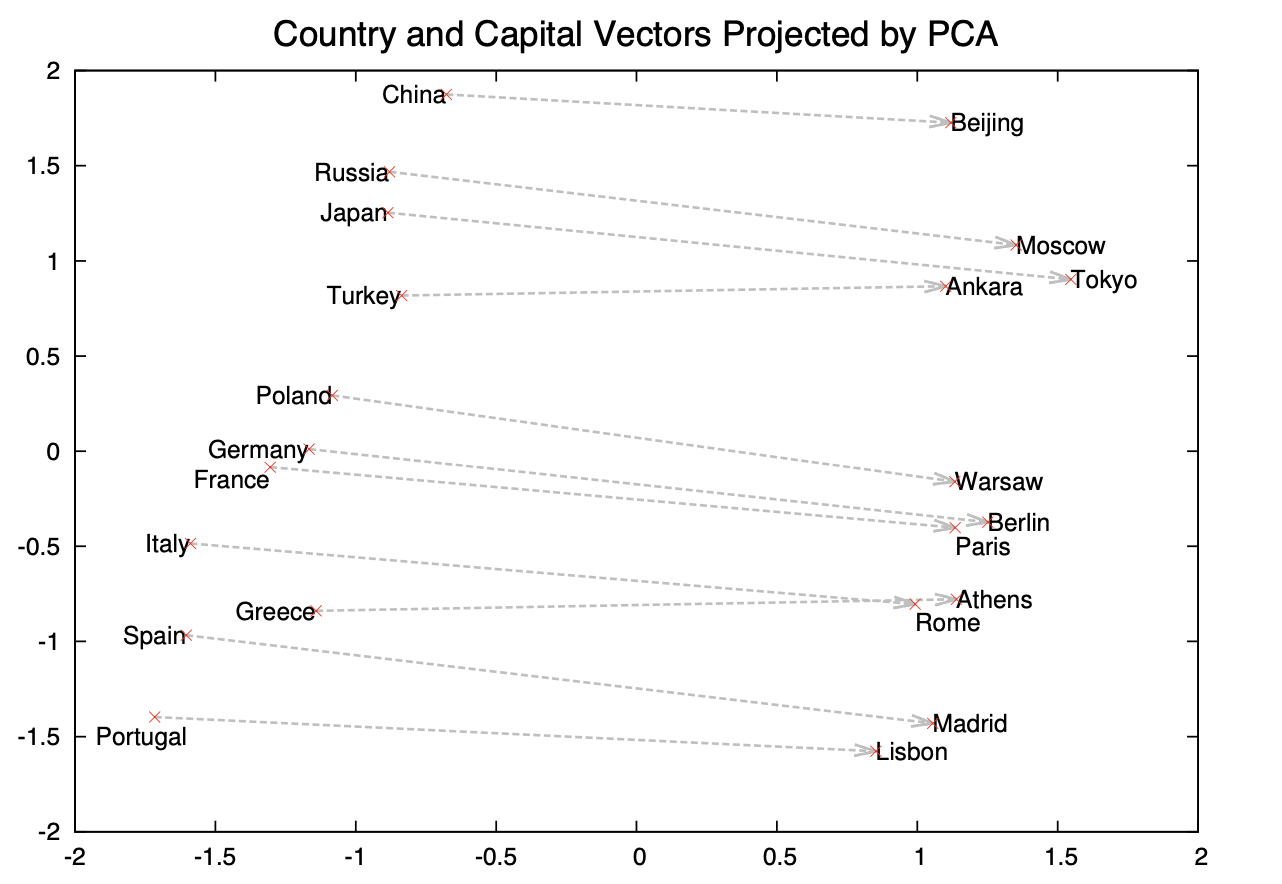
위 그림은 1000차원으로 학습된 Word2Vec의 단어 임베딩 벡터들을 PCA를 통해 2차원 공간으로 투영하여 2차원 좌표계를 통한 그림으로 그림 것이다. 기본적으로 국가와 그 수도 사이의 관계를 나타내는데 국가-수도 차이 벡터들이 거의 유사한 벡터인 것을 확인할 수 있다. 관련 논문 저자들에 따르면 더 큰 말뭉치를 활용하여 훈련을 진행한다면 더 미묘한 Analogy까지 잡아내는 모델을 획득할 수 있다고 한다.

참고 자료

수정 사항

  • 2023.02.20
    • 최초 게제
  • 2023.02.23
    • 이진 트리 및 허프만 코딩 내용 추가
  • 2023.02.24
    • Hierarchical Softmax 내용 추가
    • Nagative Sampling 내용 추가
  • 2023.02.24
    • Subsampling of Frequent Words 내용 추가
    • Word Analogy 내용 추가
  • 2023.11.19
    • 목차 추가

Go back to the List of Studies