이전 포스트는 기계 학습을 다루기 위한 기본적인 확률론 내용들을 다뤘다. 이번 포스트에서는 Class-conditional Density를 통해 데이터의 생성 방식을 고려하는 생성 모델에 대해서 이산 데이터를 바탕으로 정리하고 이를 통한 분류 문제 해결 방식에 대해서 정리한다.
Concept Learning
Concept Learning이란 양성 표본(Positive Sample)과 음성 표본(Nagative Sample)으로부터 이진 분류를 수행을 학습하는 과정을 말한다. 심리학에서는 사람은 양성 표본만을 가지고도 Concept Learning을 수행할 수 있다고 한다. 하지만 주어진 양성 표본 하나만을 가지고 예측을 수행하는 것은 매우 애매모호하다. 따라서 우리는 양성 표본만을 가지고도 학습을 수행하는 방법들을 다뤄볼 것이다. 이를 위해서는 Bayesian Concept Learning이라는 개념을 도입해야 한다.
Concept Learning에서 풀고자 하는 문제를 정의해보자. 먼저 어떤 함수 \(f\)는 주어진 표본 \(x\)에 대해서 \(x\)가 개념 \(C\)의 표본이라면 \(f(x)=1\), 그렇지 않다면 \(f(x)=0\)을 만족한다고 정의하자. Concept Learning의 목표는 이러한 함수 \(f\)를 학습하는 것이다. 이러한 문제는 이진 분류(Binary Classification) 문제라고도 한다.
이진 분류 문제를 해결하기 위해서는 일반적으로 양성 표본과 음성 표본 둘 다를 필요로 한다. 하지만 앞에서 언급했듯이 우리는 양성 표본만을 가지고도 이진 분류 문제를 접근할 수 있는 방법을 찾으려고 한다.
주어진 하나의 양성 표본만을 가지고 예측을 수행한다고 해보자. 이 경우 우리는 표본들 사이의 유사도를 측정하여 이 문제를 해결하고 싶을 것이다. 즉 양성 표본과 유사한 표본들에 대해서는 양성 표본이라고 결론지음으로서 이 문제를 접근하고자 할 것이다.
이러한 유사도를 표현하는 방법으로는 확률 분포 \(p(\tilde{x} \vert \mathcal{D})\), 즉 주어진 데이터 \(\mathcal{D}\)에 대한 새로운 표본 \(\tilde{x}\)가 \(\tilde{x}\in C\)를 만족하는 확률 분포가 있을 수 있다. 이는 추후에 이야기하겠지만 Posterior Predictive Distribution이라고 정의한다. 또한 유사도는 은닉 개념 \(C\)에 대한 추측을 통해서도 획득을 할 수 있을 것이다. 이는 가설(Hypothesis)에 대한 귀납적 추론이라고 한다.
그렇다면 우리는 어떻게 증거(Evidence) \(\mathcal{D}\)를 동일하게 만족하는 수많은 가설들 중에서 어떤 것을 가장 좋은 가설로 선택할 수 있을까? 이를 위해서는 Bayesian 접근법이 필요하다.
Bayesian Satatistics
먼저 Bayesian Probability란 확률을 어떤 현상에 대한 빈도수 대신 지식의 상태 혹은 개인의 믿음에 대한 크기를 나타내는 합리적인 기대값으로의 확률에 대한 해석이다. 확률에 대한 Bayesian Interpretation은 가설을 추리하는 명제 논리에 대한 확장으로 볼 수 있다.
Bayesian Statistics는 확률을 어떤 사건에 대한 믿음의 정도(Degree of Belief)로 표현하는 Bayesian Interpretation의 관점을 바탕으로 연구를 수행하는 통계학의 한 분야이다. 믿음의 정도는 아마 사건에 대한 사전 지식(Prior Knowledge)이 될 것이다. 예를 들면, 이전 실험들의 결과라던가 그 사건에 대한 개인적인 믿음 같은 것들이 이러한 사전 지식으로 들 수 있을 것이다.
Bayesian 통계 방법론들은 Bayes 정리를 새로운 데이터를 획득한 이후에 기존 확률값들을 계산하고 갱신하는데 적극적으로 활용한다. 이 경우에 Bayesian Statistics는 확률을 믿음의 정도로 다루기 때문에 Bayes 정리에서 사용될 매개변수 또는 매개변수 집합에 대한 믿음을 정량화하는 확률 분포에 해당하는 확률 변수를 직접 할당할 수 있는 것이다.
쉽게 다시 설명하면, 새로운 데이터 \(\mathcal{D}\)를 증거로 삼아서 매개변수 \(\theta\)에 대한 믿음의 정도를 갱신하고자 한다. 이는 아래와 같은 Bayes 정리를 통해서 수행될 수 있다:
\[p(\theta \vert \mathcal{D}) = \frac{p(\mathcal{D} \vert \theta)p(\theta)}{p(\mathcal{D})}.\]여기서 확률 분포 \(p(\theta \vert \mathcal{D})\) 및 \(p(\theta)\)를 할당하기 위해서는 빈도수로써의 확률 관점으로는 불가능하다. 대신 Bayesian 관점을 통해서 확률 분포 \(p(\theta \vert \mathcal{D})\) 및 \(p(\theta)\)를 각각 믿음의 정도로 본다면 이 믿음의 정도를 할당하여 해당 계산을 수행할 수 있다.
가설 공간
대부분의 지도 학습 알고리즘들은 가설 공간(Hypothesis Space)로부터 가능한 가설을 찾아내어 입력을 적절한 출력으로 매핑해주는 것을 주된 목표로 한다. 여기서 가설 공간은 가능한 가설들의 집합으로 정의한다. 가설이란 지도 학습 알고리즘에서 주어진 증거를 묘사하는 함수이다.
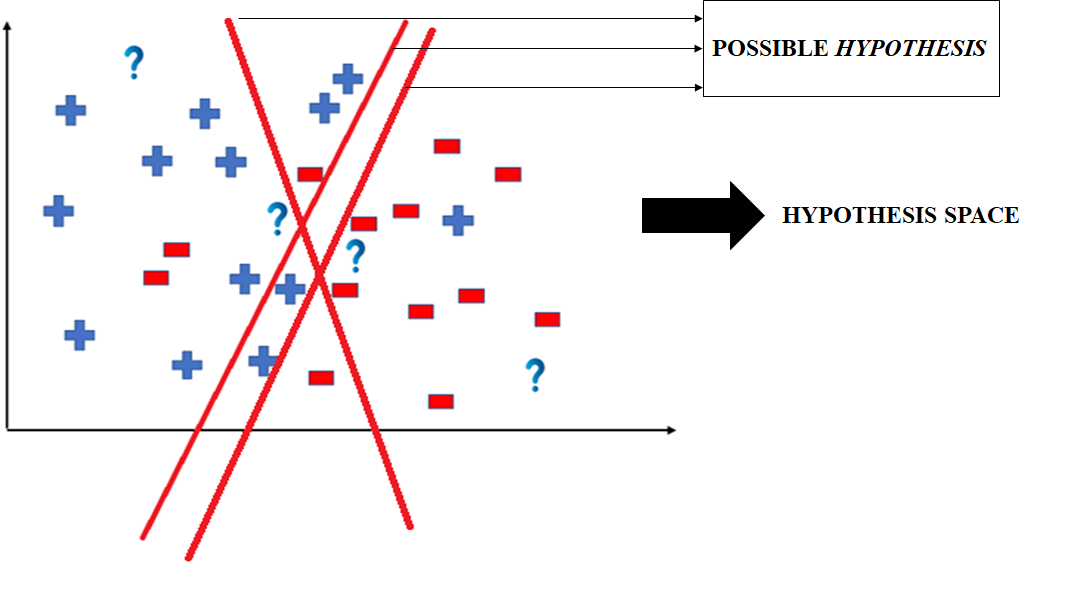
위 그림에서는 양성 표본과 음성 표본을 분류하는 지도 학습을 수행하는 과정을 예시로 든다. 양성 표본과 음성 표본은 선형 분류 기준을 통해서 분류될 것이라고 생각할 수 있다. 이 경우 가능한 가설들은 그림에서 표시된 3가지를 들 수 있을 것이다. 이러한 가설들은 각각이 증거로 나타나는 표본들을 양성/음성으로 분류하여 묘사할 수 있는 함수로 생각할 수 있다.
가능도
어떤 표본 \(\tilde{x}\in \{1, 2, \cdots, 100 \}\)가 개념 \(C\)에 속하는지를 분류하는 Concept Learning을 하나 생각해보자. 우리는 이 경우 가능한 가설을 다음의 두 가지를 들 수 있다.
\[\begin{array}{rl} h_{\text{two}} & \triangleq \text{"powers of two}, \\ h_{\text{even}} & \triangleq \text{"even numbers}. \end{array}\]이후 어떤 증거 \(\mathcal{D}=\{16, 8, 2, 64 \}\)를 관찰했다고 해보자. 우리가 방금 생각한 두 가지 가설 모두 이 증거 \(\mathcal{D}\)를 잘 부합하는 것을 확인할 수 있다. 가설을 고려했을때, 어떤 가설은 우연히 증거에 부합할 수도 있고, 어떤 가설은 자연스럽게 부합할 수 있을 것이다.
예를 들어서 다음과 같은 새로운 가설을 생각해보자:
\[h' \triangleq \text{powers of two except 32}.\]이 가설은 물론 증거 \(\mathcal{D}\)에 부합하지만 우리는 직관적으로 \(h'\)은 상당히 우연적으로 부합하는 것으로 의심할 수 있다. 우리는 이러한 우연을 최대한 제거하여 가설을 선택하고 싶을 것이다.
주어진 증거 \(\mathcal{D}\) 및 가설 \(h\)에 대한 가능도(Likelihood)는 \(h\)를 통해서 증거 \(\mathcal{D}\)가 생성될 확률 분포 \(p(\mathcal{D} \vert h)\)로 정의한다. 이 정의를 바탕으로 위에서 정의했던 가설들인 \(h_{\text{two}}\)와 \(h_{\text{even}}\)에 대한 가능도는 각각 다음과 같이 계산될 수 있다:
이 결과를 통해 우리는 \(p(\mathcal{D} \vert h_{\text{two}})\)가 \(p(\mathcal{D} \vert h_{\text{even}})\)보다는 크다는 것을 확인할 수 있다. 즉, 모델은 \(h_{\text{two}}\)를 선호한다고 결론내릴 수 있을 것이다.
두 가설들 중 \(h_{\text{two}}\)가 \(h_{\text{even}}\)보다 더 선호되는 이유는 무엇일까? Occam's Razor에서는 이를 모델은 데이터(증거)에 부합하는 가설들 중 가장 간단한(가장 작은) 가설을 선호한다고 주장한다. 이 경우에는 \(h_{\text{two}}\)될 것이다.
사전 확률
위에서 예시를 들었던 가설을 다시 떠올려보자. 주어진 데이터 \(\mathcal{D}=\{16, 8, 2, 64\}\)에 대해서 개념 \(h'=\text{powers of two except 32}\)보다는 \(h=\text{powers of two}\)가 직관적으로 좀 더 그럴듯할 것이다.
그렇다면 그 이유는 무엇일까? \(h'\)은 왜 굳이 \(32\)가 빠지는 우연에 대한 설명을 필요로 한다. 즉 개념적으로 부자연스러운 개념이라는 것이다. 우리는 직관적으로 이러한 부자연스러운 개념에게는 낮은 사전 확률(Prior Probability)을 할당할 수 있다.
이러한 사전 확률의 할당 방식은 매우 주관적일 수 있다. 하지만 매우 유용하다. 일단 사전 확률을 다루는 방식은 배경 지식을 통해서 우리가 풀어야 하는 문제를 접근한다는 점에서 합리적이라고 볼 수 있다. 이는 또한 학습 과정에서 학습 속도를 매우 증가시켜 준다는 좋은 장점이 있다.
사후 확률
사후 확률 간단하게 가능도와 사전 확률의 곱으로 정의된다:
\[p(h\vert \mathcal{D}) = \frac{p(\mathcal{D} \vert h)p(h)}{\sum_{h'\in \mathcal{H}}p(\mathcal{D}, h')} = \frac{p(\mathcal{D} \vert h)p(h)}{p(\mathcal{D})}.\]여기서 \(\mathcal{H}\)는 가설 공간이다.
사후 확률은 세상에 대한 우리의 내적 믿음이라고 볼 수 있다. 부자연스러운 개념인 \(\text{"powers of 2, plus 37"}\), 또는 \(\text{"powers of 2, except 32"}\)는 높은 가능도에도 불구하고 낮은 사전 확률로 인하여 낮은 사후 확률을 갖게 된다.
일반적으로 사후 확률은 데이터가 충분히 많아짐에 따라서 어떤 하나의 개념에서 피크를 찍게 되는 경향이 있다. 이를 MAP Estimator라고 한다:
여기서 \(\hat{h}_{\text{MAP}} = \arg \max_h p(h \vert \mathcal{D})\)는 사후 최빈값(Posterior Mode)이고 \(\delta\)는 Dirac Measure이다.
참고 자료
- Machine Learning: A Probabilistic Perspective
- Wikipedia
- https://www.geeksforgeeks.org/ml-understanding-hypothesis/
수정 사항
- 2022.07.17
- 최초 게제
- 2022.07.23
- Concept Learning, 가설 공간, 가능도 내용 정리
- 2022.07.24
- 사전 확률, 사후 확률 내용 정리