이전 포스트에서 Clique Factorization을 통해서 Gibbs Distribution를 통해 Markov Random Field (MRF)의 모형화 과정을 간단하게 소개했다. 이번 포스트에서는 Factorization Graph를 통해서 MRF를 표현하는 방식과 Bayesian Network에서의 적용을 통해서의 활용 예시를 들어보도록 하겠다.
Factor Graph
먼저 Factor를 명확하게 정의하자. Factor는 Ensemble을 이루고있는 시스템의 각각의 상태값에 대한 함수로 정의된다:
\[\phi: \text{Val}(X) \rightarrow \mathbb{R}^+.\]여기서 \(X=\{X_1, \cdots, X_N\}\)은 Random Variable들의 집합이다.
그렇다면 Factor Graph는 무엇일까? 만약 주어진 Random Variable 집합 \(X=\{X_1, \cdots, X_N\}\)가 MRF를 형성한다면 그에 해당하는 Undirected Graph \((V, E)\)가 존재할 것이다. 만약 주어진 Factor 집합 \(\Phi=\{\phi_a\}_{a\in F}\)에 대해서 Bipartite Graph \(G=(V, F, E)\)를 그린다면 그 Graph를 우리는 Factor Graph라고 부른다.
여기서 Factor Graph \(G\)는 \(V\)와 \(F\)의 원소들이 각각 서로 연관이 있는 경우에만 Edge로 연결되게 된다.
조금 더 이해를 돕기 위해서 이전 포스트에서 등장했던 지각 모형을 이용하여 예시를 들어보도록 하자.
Factor Graph: Example
일단 지각 모형은 Bayesian Network를 설명하기 위한 모형이었지만, 사실 Bayesian Network도 MRF의 한 종류라고 봐도 될 것이다.
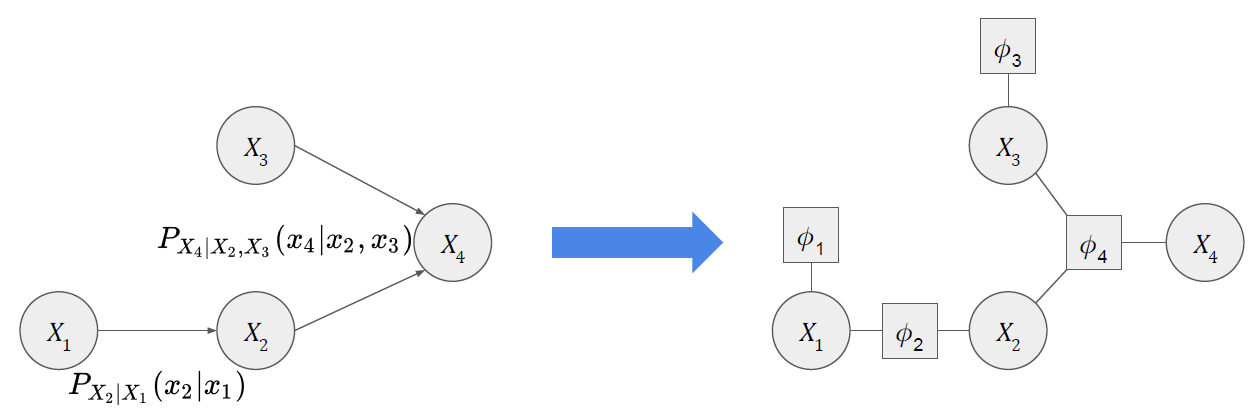
먼저 각 Node들은 그대로 Node로 둔 상태에서 Factor가 어떻게 정의될 수 있는지 살펴봐야 할 것이다. Bayesian Network에서 Factor는 다음과 같다.
\[\begin{array}{rl} \phi_1(x_1) & = P_{X_1}(x_1) \\ \phi_2(x_1, x_2) & = P_{X_2|X_1}(x_2|x_1) \\ \phi_3(x_3) & = P_{X_3}(x_3) \\ \phi_4(x_2, x_3, x_4) & = P_{X_4|X_2, X_3}(x_4|x_2, x_3) \end{array}\]이를 바탕으로 Factor Graph를 그리면 아래와 같을 것이다.
References
- Introduction to Statistical Relational Learning
- Information, Physics, and Computation
- Probabilistic Graphical Models