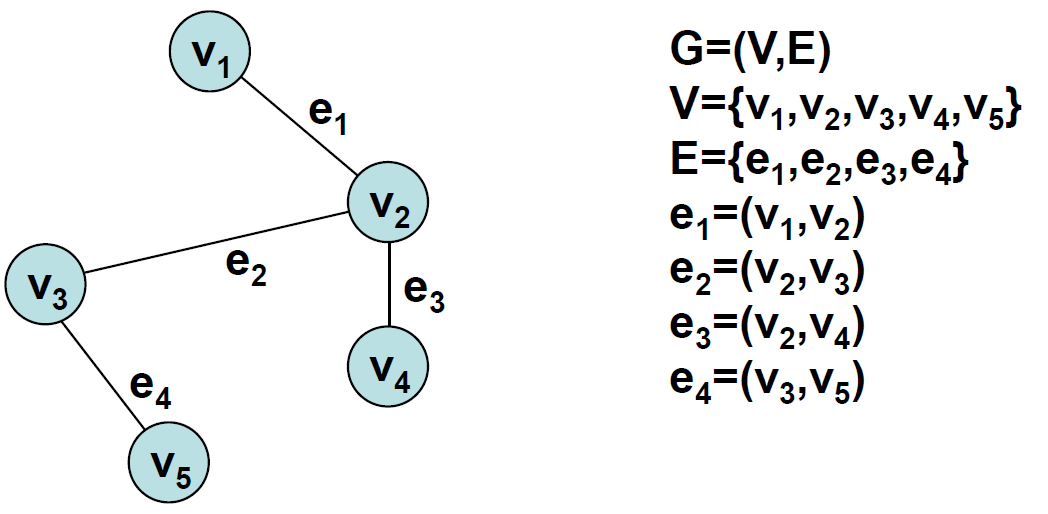
#graphical model #statistics #machine learning

Graph

Graph란 Node와 Edge로 이루어진 구조를 말한다. 일반적으로 Graph를 정의하기 위해서는 Node 집합 \(V\)와 Edge 집합 \(E\)가 먼저 정의되어야 한다. Edge는 하나의 Node 쌍에 대해서 정의가 되게 되며 Node 두 개를 연결하는 개념으로 생각할 수 있다.

어쩄든 Graph \(G\)는 \(G=(V, E)\)의 순서쌍으로 정의가 된다.

특히, Edge에 방향이 있는 경우를 Directed Graph라고 부르게 된다.

그렇다면 Graph는 왜 사용하는 것일까? 보통 Graph를 사용하는 경우는 여러 요소들 사이의 상관관계를 시각화하고 그 관계를 Formal하게 다루고자하는 경우에 사용하게 된다.

(그림 출처: https://ratsgo.github.io/data%20structure&algorithm/2017/11/18/graph/)

Graphical Model

Graphical Model (Probabilistic Graphical Model, Structured Probabilistic Model)은 보통 랜덤 변수 (Random Variable)들 사이의 Conditional Dependency 구조를 표현하기 위해서 많이 사용되게 된다. 대표적인 예시로는 Bayesian Network가 있는데 Bayesian Network에서 Node는 랜덤 변수, Edge는 그 랜덤 변수 사이의 조건부 확률로 정의가 되게 된다.

크게 두 종류로 나뉘게 되는데 먼저 방금 언급했던 Bayesian Network가 있고 또 다른 하나는 Markov Random Field가 있다. 각각 Bayesian Network는 Directed Graph, Markov Random Field는 Undirected Graph의 구조를 갖는다.

Bayesian Network

Bayesian Network는 기본적으로 Directed Acyclic Graph (DAG) 구조를 가지게 된다. Node는 랜덤 변수를 나타내며, Edge는 두 랜덤 변수 사이의 방향성을 지닌 영향력, 즉 Conditional Probability Distribution (CPD)을 나타내게 된다. 방향성이 있는 이유는 CPD가 방향성을 지니기 때문에 그러한 것이다.

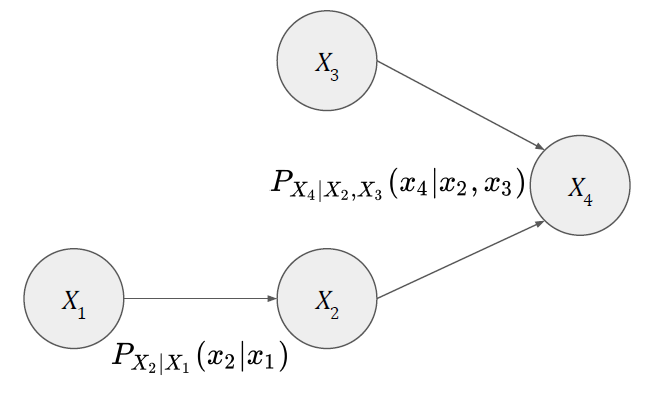
Bayesian Network: Example

다음과 같은 예시를 생각해보자. 나는 지각을 너무 자주한다. 어느날 내가 더이상 지각을 하지 않기를 바라는 마음에서 친구가 나에게 내기를 제안한다. 내가 다음날 또 지각을 한다면 친구의 승, 지각을 하지 않는다면 내가 승리하는 내기이다. 나는 이 내기를 참여할지 말지를 내가 지각할 확률에 기반하여 결정을 하고싶다. 따라서 나는 자신이 지각하는 원인들을 파악하고 다음날 지각할 확률을 Bayesian 관점에서 구해보려고 시도한다.

내가 고민해본 결과, 나의 지각 원인은 다음과 같은 총 세 가지 변수를 들 수 있다고 결론을 내렸다:

  • 알람이 제대로 울렸는가? Yes/No: 랜덤 변수 \(X_1\)
  • 늦잠을 잤는가? Yes/No: 랜덤 변수 \(X_2\)
  • 1호선이 제때 왔는가? Yes/No: 랜덤 변수 \(X_3\)

우리는 이 세 가지 랜덤 변수를 바탕으로 네 번째 랜덤 변수 \(X_4\) (지각을 하였는가? Yes/No)에 대한 Marginal Distribution을 추론하고자 한다.

\[P_{X_4}(x_4) = \sum_{x_1, x_2, x_3} P_{X_1, X_2, X_3, X_4}(x_1, x_2, x_3, x_4)\]

이러한 Marginalization 계산을 위해서는 Joint Distribution \(P_{X_1, X_2, X_3, X_4}\)에 대한 추론이 선행되어야 할 것이다. 이를 위해서는 각각의 랜덤 변수에 대한 가정이 필요하다. Bayesian 관점에서 나의 가정들은 아래와 같다:

  • 알람과 1호선은 서로 독립적인 사건:
    • 알람이 제대로 울릴 것인가에 대한 나의 믿음: 0.9
    • 1호선이 제때 올 것인가에 대한 나의 믿음: 0.2
  • 늦잠은 알람에 의존적인 사건:
    • 늦잠을 잘 것인가에 대한 나의 믿음:
      • 알람이 제대로 울리면 0.1
      • 알람이 제대로 울리지 않으면 0.7
  • 지각은 늦잠과 1호선에 의존적인 사건:
    • 늦잠을 안자고 1호선이 제때 오면 0.2
    • 늦잠을 안자고 1호선이 제떄 안오면 0.7
    • 늦잠을 자고 1호선이 제때 오면 0.8
    • 늦잠을 자고 1호선이 제때 안오면 0.9

이러한 가정들을 바탕으로 다음과 같은 Bayesian Network를 그릴 수 있다.

또한 가정을 바탕으로 Edge 값인 CPD들을 아래와 같이 정의할 수 있다.

\[P_{X_1}(x_1) = \left\{ \begin{array}{ll} 0.9 & \text{if} \ x_1=1, \\ 0.1 & \text{otherwise}. \end{array} \right.\] \[P_{X_2|X_1}(x_2|x_1) = \left\{ \begin{array}{ll} 0.3 & \text{if} \ x_1=0, x_2=0, \\ 0.7 & \text{if} \ x_1=0, x_2=1, \\ 0.9 & \text{if} \ x_1=1, x_2=0, \\ 0.1 & \text{if} \ x_1=1, x_2=1. \end{array} \right.\] \[P_{X_3}(x_3) = \left\{ \begin{array}{ll} 0.2 & \text{if} \ x_3=1, \\ 0.8 & \text{otherwise}. \end{array} \right.\] \[P_{X_4|X_2,X_3}(x_4|x_2,x_3) = \left\{ \begin{array}{ll} 0.3 & \text{if} \ x_2=0, x_3=0, x_4=0, \\ 0.7 & \text{if} \ x_2=0, x_3=0, x_4=1, \\ 0.8 & \text{if} \ x_2=0, x_3=1, x_4=0, \\ 0.2 & \text{if} \ x_2=0, x_3=1, x_4=1, \\ 0.1 & \text{if} \ x_2=1, x_3=0, x_4=0, \\ 0.9 & \text{if} \ x_2=1, x_3=0, x_4=1, \\ 0.2 & \text{if} \ x_2=1, x_3=1, x_4=0, \\ 0.8 & \text{if} \ x_2=1, x_3=1, x_4=1. \\ \end{array} \right.\]

이 모형은 앞으로도 계속 등장할 예정이며 지각 모형이라고 부르도록 하겠다.

Factorization

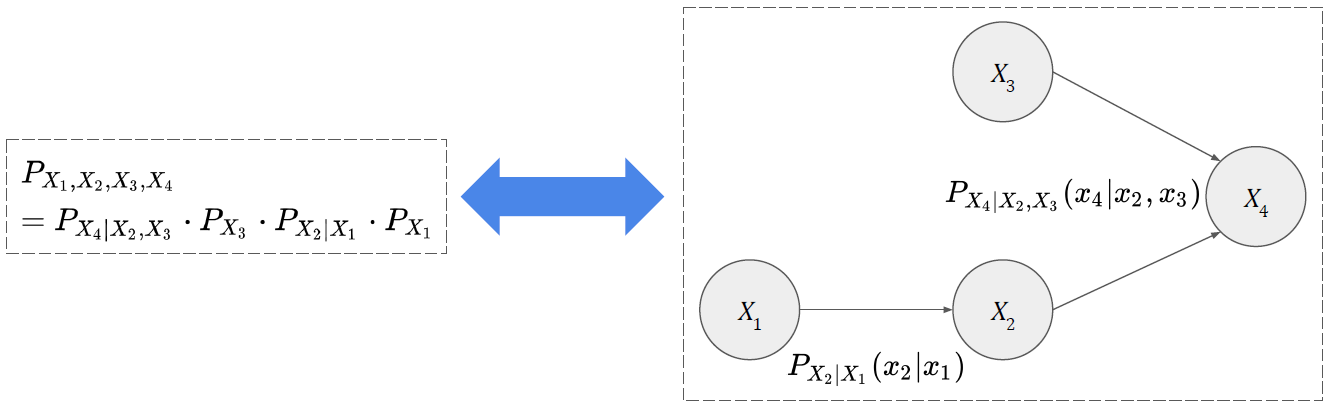
이제 Bayes Rule을 이용하여 Joint Distribution을 추론해보자. 우리의 목적은 \(X_4\)에 대해서 Probability Distribution을 쓰는 것이기 때문에 다음과 같은 방식으로 Joint Distribution을 써보는 것을 시도한다.

\[\begin{array}{rl} P_{X_1, X_2, X_3, X_4}(x_1, x_2, x_3, x_4) & = P_{X_4|X_1, X_2, X_3}(x_4|x_1, x_2, x_3)\cdot P_{X_1, X_2, X_3}(x_1, x_2, x_3) \\ & = P_{X_4|X_1, X_2, X_3}(x_4|x_1, x_2, x_3)\cdot P_{X_3|X_1, X_2}(x_3|x_1, x_2) \cdot P_{X_1, X_2}(x_1, x_2) \\ & = P_{X_4|X_1, X_2, X_3}(x_4|x_1, x_2, x_3)\cdot P_{X_3|X_1, X_2}(x_3|x_1, x_2) \cdot P_{X_2|X_1}(x_2|x_1) \cdot P_{X_1}(x_1) \\ & = P_{X_4|X_2, X_3}(x_4|x_2, x_3) \cdot P_{X_3}(x_3) \cdot P_{X_2|X_1}(x_2|x_1) \cdot P_{X_1}(x_1) \end{array}\]

특히 여기서 마지막 두 줄은 Bayesian Network를 다룰때 활용되는 중요한 가정인 Local Markov Assumption을 사용하는 부분이다. 이것은 잠시 후에 다뤄볼 것이다.

\[\begin{array}{l} P_{X_4|X_1, X_2, X_3}(x_4|x_1, x_2, x_3)\cdot P_{X_3|X_1, X_2}(x_3|x_1, x_2) \cdot P_{X_2|X_1}(x_2|x_1) \cdot P_{X_1}(x_1) \\ \ \ \ \ = P_{X_4|X_2, X_3}(x_4|x_2, x_3) \cdot P_{X_3}(x_3) \cdot P_{X_2|X_1}(x_2|x_1) \cdot P_{X_1}(x_1) \end{array}\]

어쨌든 최종적으로 구한 Joint Distribution은 아래와 같다.

\[P_{X_4|X_2, X_3}(x_4|x_2, x_3) \cdot P_{X_3}(x_3) \cdot P_{X_2|X_1}(x_2|x_1) \cdot P_{X_1}(x_1)\]

이런 방식으로 Joint Distribution을 각 랜덤 변수에 대한 CPD들에 대한 곱으로 써놓는 것을 Factorization이라고 정의한다. 이것을 Bayesian Network의 관점에서 다시 정의하면 다음과 같다:

\[P_{X_1, \cdots, X_N} = \prod_{i=1}^n P_{X_i|\mathbf{Pa}(X_i)}\]

\(X_1\)과 \(X_3\)은 Parent Node가 없기 때문에 단독으로 Distribution을 쓸 수 있고 (\(P_{X_1}, P_{X_3}\)), \(X_2\)의 Parent Node는 \(X_1\), \(X_4\)의 Parent Node는 \(X_2, X_3\)이므로 \(P_{X_2 \vert X_1}\), \(P_{X_4 \vert X_2, X_3}\)로 쓴 것을 확인할 수 있다.

최종적으로 위의 결과들을 바탕으로 Marginal Distribution을 추론해보도록 하자.

\[\begin{array}{ll} P_{X_4}(x_4) & = \sum_{x_1, x_2, x_3} P_{X_1, X_2, X_3, X_4}(x_1, x_2, x_3, x_4) \\ & = \sum_{x_3} \sum_{x_2} P_{X_4|X_2, X_3}(x_4|x_2, x_3) \cdot P_{X_3}(x_3) \sum_{x_1} P_{X_2|X_1}(x_2|x_1) \cdot P_{X_1}(x_1) \\ & = \sum_{x_3} \sum_{x_2} P_{X_4|X_2, X_3}(x_4|x_2, x_3) \cdot P_{X_3}(x_3) \cdot \left[0.9 \cdot P_{X_2|X_1=1}(x_2) + 0.1 \cdot P_{X_2|X_1=0}(x_2) \right] \\ & = 0.9 \cdot \left[ 0.2 \cdot 0.1 \cdot P_{X_4|X_2=1, X_3=1}(x_4) + 0.8 \cdot 0.1 \cdot P_{X_4|X_2=1, X_3=0}(x_4) \right. \\ & \ \ \ \ \ \ \ \ \ \ \ \ + \left. 0.2 \cdot 0.9 \cdot P_{X_4|X_2=0, X_3=1}(x_4) + 0.8 \cdot 0.9 \cdot P_{X_4|X_2=0, X_3=0}(x_4) \right] \\ & \ \ \ \ + 0.1 \cdot \left[ 0.2 \cdot 0.7 \cdot P_{X_4|X_2=1, X_3=1}(x_4) + 0.8 \cdot 0.7 \cdot P_{X_4|X_2=1, X_3=0}(x_4) \right. \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ + \left. 0.2 \cdot 0.3 \cdot P_{X_4|X_2=0, X_3=1}(x_4) + 0.8 \cdot 0.3 \cdot P_{X_4|X_2=0, X_3=0}(x_4) \right] \\ & = 0.032 \cdot P_{X_4|X_2=1, X_3=1}(x_4) + 0.128 \cdot P_{X_4|X_2=1, X_3=0}(x_4) \\ & \ \ \ \ + 0.168 \cdot P_{X_4|X_2=0, X_3=1}(x_4) + 0.672 \cdot P_{X_4|X_2=0, X_3=0}(x_4) \end{array}\]

따라서 최종적인 Marginal Distribution은:

\[P_{X_4}(x_4) = \left\{ \begin{array}{ll} 0.032 \cdot 0.8 + 0.128 \cdot 0.9 + 0.168 \cdot 0.2 + 0.672 \cdot 0.7 = 0.6448 & \text{if} \ x_4=1, \\ 0.032 \cdot 0.2 + 0.128 \cdot 0.1 + 0.168 \cdot 0.8 + 0.672 \cdot 0.3 = 0.3552 & \text{otherwise}. \end{array} \right.\]

즉, Bayesian 관점에서 지각을 할 것이냐에 대한 나의 믿음은 0.6448이므로 이 내기는 내가 불리하기 때문에 내기를 안하는 것이 이득이라고 결론을 내리게 된다.

Local Markov Assumption

지금까지의 과정에서 몇 가지 의문점이 생길 수 있다. 먼저 같은 구조의 Bayesian Network는 항상 같은 Factorization 결과를 도출할 것인가? 또는 반대로 같은 Factorization 결과를 가지는 Bayesian Network들은 모두 같은 구조를 가지게 될까?

이러한 의문점들을 해소할 수 있는 가정, 또는 성질이 Local Markov Assumption이다.

Local Markov Assumption은 다음과 같이 정의된다. 주어진 Bayesian Network에서 Node에 해당하는 Random Variable은 자신의 Parent Node가 관찰이 된다면 자신의 Child Node가 아닌 Random Variable들과 독립 관계를 가지게 된다. 즉, 모든 Random Variable들은 자신의 Parent Node가 주어졌을 때 자신의 Child Node들을 제외한 모든 Random Variable들과 조건부 독립 관계를 갖는다. 이것을 수식으로 표현하면 다음과 같다:

\[(X_i \perp \mathbf{NonDescendants}(X_i) | \mathbf{Pa}(X_i))\]

이러한 Local Markov Assumption과 관련된 중요한 정리가 있다. 증명은 여기에 따로 소개하지는 않겠다.

  • \(G\)가 랜덤 변수들의 집합 \(\{X_i \}_{i=1}^n\)에 대한 Bayesian Network Graph이고, \(P_{X_1, \cdots, X_N}\)가 그 랜덤 변수들에 대한 Joint Distribution이다. 이 경우 \(G\)에 대한 모든 Local Markov Assumption이 만족한다면 \(P_{X_1, \cdots, X_N}\)는 \(G\)에 대해서 Factorization가 될 수 있다.
  • 또한 이 명제는 역이 성립한다.

이 정리가 하고자하는 말은 Local Markov Assumption을 만족하는 경우에는 Bayesian Network와 그에 대한 Factorization 결과는 서로 동치라는 점이다.

References

Go back to the List of Studies